Một hình trụ có bán kính đáy là 3cm, chiều cao là 5cm. Tính diện tích toàn phần của hình trụ đó ...
Đọc tiếp
Một hình trụ có bán kính đáy là 3cm, chiều cao là 5cm. Tính diện tích toàn phần của hình trụ đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 4 2018
Đúng(0)
Những câu hỏi liên quan
CM
25 tháng 12 2017
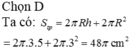
Diện tích toàn phần gấp đôi diện tích xung quanh nên:
2πRh + 2π R 2 = 2.2π R 2 => 2πRh = 2π R 2 => R = h
Vậy chiều cao của hình trụ là 3cm
2 tháng 7 2023
1:
V=pi*r^2*h
=>r^2*15*pi=375pi
=>r^2=25
=>r=5
Sxq=2*pi*r*h=2*5*15*pi=150pi
5 tháng 5 2019
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
5 tháng 5 2019
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
CM
17 tháng 9 2017
Ta có : C = 13cm, h = 3cm
Diện tích xung quanh của hình trụ là :
S Xq = 2 π r ⋅ h = Ch = 13.3 = 39 cm 2
b) Ta có : r = 5mm, h = 8mm
Thể tích hình trụ là :
V = π r 2 h = π ⋅ 5 2 ⋅ 8 = 200 π ≈ 628 mm 3
1 tháng 4 2023
\(S_{XQ}=\left(5+12+13\right)\cdot8=8\cdot26=204\left(cm^2\right)\)
\(S_{TP}=204+2\cdot5\cdot12\cdot2=204+4\cdot60=204+240=444\left(cm^2\right)\)
\(V=5\cdot12\cdot8=60\cdot8=480\left(cm^3\right)\)