Cho hàm số y = 2 x + 2 x - 1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến tạo với hai tiệm cận một tam giác có chu vi nhỏ nhất.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


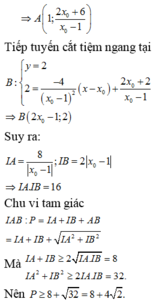
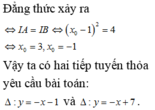

+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
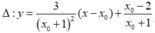
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có 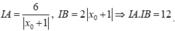
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
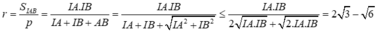
Suy ra,
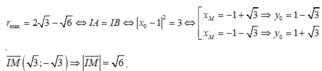
Chọn D.

Vì tam giác IAB cân tại I nên tiếp tuyến phải song song với một trong 2 đường thẳng có phương trình \(y=x;y=-x\).
Ta có \(y'=\frac{1}{\left(x+2\right)^2}>0;x\ne-2\)
Mọi \(M\left(x_0;y_0\right)\) là tiếp điểm thì \(y'\left(x_0\right)=1\Leftrightarrow1=\frac{1}{\left(x_0+2\right)^2}\Leftrightarrow\left[\begin{array}{nghiempt}x_0=-1\\x_0=-3\end{array}\right.\)
Từ đó suy ra 2 tiếp tuyến là \(y=x+1;y=x+5\)

- Hàm số đã cho xác định với ∀x ≠ 1.
- Ta có:
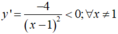
- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm, suy ra phương trình tiếp tuyến của (C):
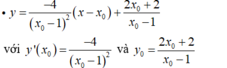
- Tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân nên hệ số góc của tiếp tuyến bằng ± 1. Mặt khác: y ' ( x 0 ) < 0 , nên có: y ' ( x 0 ) = - 1 .
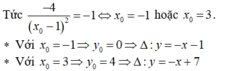
- Vậy, có 2 tiếp tuyến thỏa mãn đề bài: y = -x - 1; y = -x + 7.
Chọn D

Chọn đáp án B
![]()
Đạo hàm
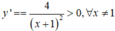
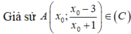
Đường thẳng ∆ là tiếp tuyến của đồ thị (C) tại ∆ nên có hệ số góc là
Phương trình ∆
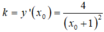
![]()
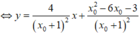
Đồ thị (C) có đường tiệm cận đứng là ∆ 1 : x = - 1 và đường tiệm cận ngang là ∆ 2 : y = 1
![]()
![]()
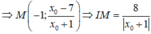
![]()
![]()
Nửa chu vi tam giác IMN là
![]()
Dấu "=" xảy ra khi
![]()
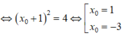
Bán kính đường tròn nội tiếp tam giác IMN là
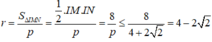

Đáp án C.
Ta có I 2 ; 1 .
Tiếp tuyến với C tại điểm M x 0 ; x 0 + 2 x 0 − 2 là d : y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2
Tọa độ A là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 x = 2 ⇒ y = 4 x 0 − 2 + x 0 + 2 x 0 − 2 ⇒ A 2 ; x 0 + 6 x 0 − 2 ⇒ I A → = 0 ; 8 x 0 − 2
Tọa độ B là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 y = 2 ⇒ x 0 − 2 2 = − 4 x − x 0 + x 0 2 − 4 ⇒ B 2 x 0 − 2 ; 1 ⇒ I B → = 2 x 0 − 4 ; 0 Do đó C I A B = π . A B = π I A 2 + I B 2 ≥ π 2 I A . I B
Mà I A . I B = 8 x 0 − 2 . 2 x 0 − 4 = 16 ⇒ C I A B ≥ 4 π 2