Đẳng thức nào trong các đẳng thức sau đúng?
A. 1 + i 2018 = 2 2019 . i
B. 1 + i 2018 = - 2 2019 . i
C. 1 + i 2018 = - 2 2019
D. 1 + i 2018 = - 2 1009
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
NB
1
KV
16 tháng 10 2023
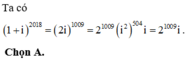
(x + y)²⁰¹⁸ + 4|y + 1/2| = 0
⇒ (x + y)²⁰¹⁸ = 0 và |y + 1/2| = 0
*) |y + 1/2| = 0
y + 1/2 = 0
y = -1/2
*) (x + y)²⁰¹⁸ = 0
x + y = 0
x = -y
x = 1/2
Vậy x = 1/2; y = -1/2
VT
Vũ Thị Minh Ánh
Giáo viên
2 tháng 1 2023
\(5x^2+5y^2+8xy-2x+2y+2=0\)
\(\Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
Vì \(\left(x+y\right)^2\ge0,\left(x-1\right)^2\ge0,\left(y+1\right)^2\ge0\)
\(\Rightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2\ge0\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x+y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(\left(x+y\right)^{2018}+\left(x-2\right)^{2019}+\left(y+1\right)^{2020}=\left(1-1\right)^{2018}+\left(1-2\right)^{2019}+\left(-1+1\right)^{2020}=-1\)
M
28 tháng 8 2019
B=\(x^{2019}-2019.x^{2018}+2019.x^{2017}-...+2019x-1\)
Ta có : 2019 = 1+2018=1+x ( vì x = 2018 )
Suy ra : \(x^{2019}-\left(x+1\right).x^{2018}+\left(x+1\right).x^{2017}-....+\left(x+1\right).x-1\)
=\(x^{2019}-\left(x^{2019}+x^{2018}\right)+\left(x^{2018}+x^{2017}\right)-...+\left(x^2+x\right)-1\)
= \(x^{2019}-x^{2019}-x^{2018}+x^{2018}+x^{2017}-....+x^2+x-1\)
= \(x-1\) mà x =2018
=> \(x-1=2018-1=2017\)
Vậy giá trị của biểu thức B = 2017
CM
28 tháng 5 2019
Đáp án B
Ta có: log a 3 a a 2 3 = log a 1 3 a . a 2 3 = log a 1 3 a 1 + 2 3 = 5 .
PT
1
PT
1