Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x=a và x=b (b<a) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với a ≤ x ≤ b Giả sử hàm số y=S(x) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
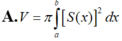

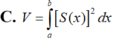
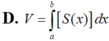

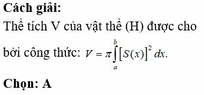

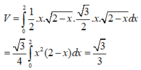

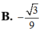
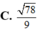


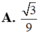
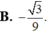
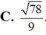
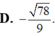


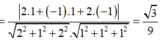

Đáp án A.