Cho cấp số cộng u n với số hạng đầu là u 1 = − 2017 và công sai d = 3. Bắt đầu từ số hạng nào trở đi mà các số hạng của cấp số cộng đều nhận giá trị dương?
A. u 674
B. u 672
C. u 675
D. u 673
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Ta có: u n = u 1 + n − 1 d = − 2017 + n − 1 .3
Số hạng nhận giá trị dương khi:
− 2017 + n − 1 .3 > 0 ⇔ n − 1 > 2017 3 ⇔ n > 673 ⇒ n = 674.

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77

Đáp án C
Số hạng tổng quát là: u n = u 1 + n − 1 d = 2018 + n − 1 − 5 = − 5 n + 2023 < 0 ⇔ n > 404 , 6 ⇒ bắt đầu từ số hạng thứ 405 thì nhận giá trị âm.

Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
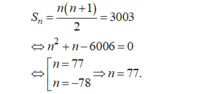

a) Ta có: \({u_n} = - 3 + \left( {n - 1} \right).5\)
b) Ta có:
\(\begin{array}{l}492 = - 3 + \left( {n - 1} \right).5\\ \Leftrightarrow n - 1 = 99\\ \Leftrightarrow n = 100\end{array}\)
492 là số hạng thứ 100 của cấp số cộng
c) Ta có: \(300 = - 3 + \left( {n - 1} \right).5 \Leftrightarrow n - 1 = 60,6\)
300 không là số hạng của cấp số cộng
Đáp án A
Công thức số hạng tổng quát là: u n = u 1 + n − 1 d = − 2017 + n − 1 .3 = 3 n − 2020.
Ta có: u n > 0 ⇔ 3 n − 2020 > 0 ⇔ n > 2020 3 ~ 673 , 3 ⇒ Bắt đầu từ số hạng u 674 các số hạng của cấp số cộng đều nhận giá trị dương.