Câu 7: Một ấm đun nước bằng điện có ghi (220V –605W) được mắc vào nguồn điện cóhiệu điện thế 220V không đổi. a) Tính điện trở của ấm đun sôi nước bằng điện .b) Dùng ấm đun sôi nước bằng điện trên để đun 2 lít nước đang ở 25oC thì sau 20 min nước sôi ở 100oC. Tìm hiệu suất của bếp. Cho nhiệt dung riêng của nước là 4200 J/(kg.K).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1.
a. Khi dòng điện đi qua ấm, điện năng đã biến thành nhiệt năng
Điện trở của dây làm ấm là: \(P=\frac{U^2}{P}=\frac{200^2}{1100}=44\Omega\)
b. Có:
\(V=1,8l\Rightarrow m=1,8kg\)
\(C=4200J/kg.K\)
\(\hept{\begin{cases}t_1=25^oC\\t_2=100^oC\end{cases}}\)
Nhiệt lượng cần thiết để đun sôi nước là: \(Q=m.C.\left(t_2-t_1\right)=1,8.4200.\left(100-25\right)=567000J\)
Thời gian để nước sôi là: \(t=\frac{Q}{P}=\frac{567000}{1100}=515,45\) giây
Bài 2.
Nhiệt lượng toả ra để đun sôi nước là: \(Q=m.c.\left(t_1-t\right)=2,5.4200.\left(100-25\right)=787500J\)
Thời gian đun nước là: \(t=\frac{Q}{P_{dm}}=\frac{787500}{900}=875s\)

Tham khảo
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp:
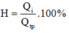
Nhiệt lượng mà ấm điện đã tỏa ra khi đó là:
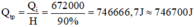
c) Từ công thức: Qtp = A = P.t
→ Thời gian đun sôi lượng nước:

Okie iem :3
\(Q=P.t=1000.t\left(J\right)\)
\(Q_{toa}=mc\left(100-20\right)=4.4200.80\left(J\right)\)
Áp dụng phương trinh cân bằng nhiệt:
\(\Rightarrow Q=Q_{toa}\Leftrightarrow1000t=4.4200.80\Rightarrow t=...\left(s\right)\)
b/ Con số 1000 W cho biết công suất của ấm khi hoạt động bình thường
c/ Điện trở được gập làm đôi, nghĩa là cắt dây đó thành 2 phần bằng nhau rồi mắc song song
\(R'=\dfrac{1}{2}R=\dfrac{1}{2}.\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{1}{2}.\dfrac{220^2}{1000}=...\left(\Omega\right)\)
\(\Rightarrow R_{td}=\dfrac{R'}{2}=...\left(\Omega\right)\Rightarrow Q'=\dfrac{U^2_{dm}}{R_{td}}.t\left(J\right)\)
\(\Rightarrow Q'=Q_{toa}\Leftrightarrow\dfrac{220^2}{R_{td}}.t'=4.4200.80\Rightarrow t'=...\left(s\right)\)

Nhiệt lượng ấm thu vào:
\(Q_{thu}=mc\Delta t=2.4200.\left(100-25\right)=630000\left(J\right)\)
Do \(H=\dfrac{Q_{thu}}{Q_{tỏa}}\Rightarrow Q_{tỏa}=\dfrac{Q_{thu}}{H}=\dfrac{630000}{80\%}=787500\left(J\right)\)
\(\Rightarrow Q_{tỏa}=A=P.t=787500\Rightarrow t=\dfrac{787500}{1000}=787,5\left(s\right)\)

a,\(=>Qthu=2.4200\left(100-20\right)=672000J\)
b,\(=>H=\dfrac{Qthu}{Qtoa}.100\%=90\%=>Qtoa=746667J\)
c,\(=>H=\dfrac{3.4200.80}{I^2Rt}.100\%=\dfrac{1008000}{\left(\dfrac{P}{U}\right)^2\left(\dfrac{U^2}{P}\right)t}.100\%=90\%\)
\(=>t=1120s\)
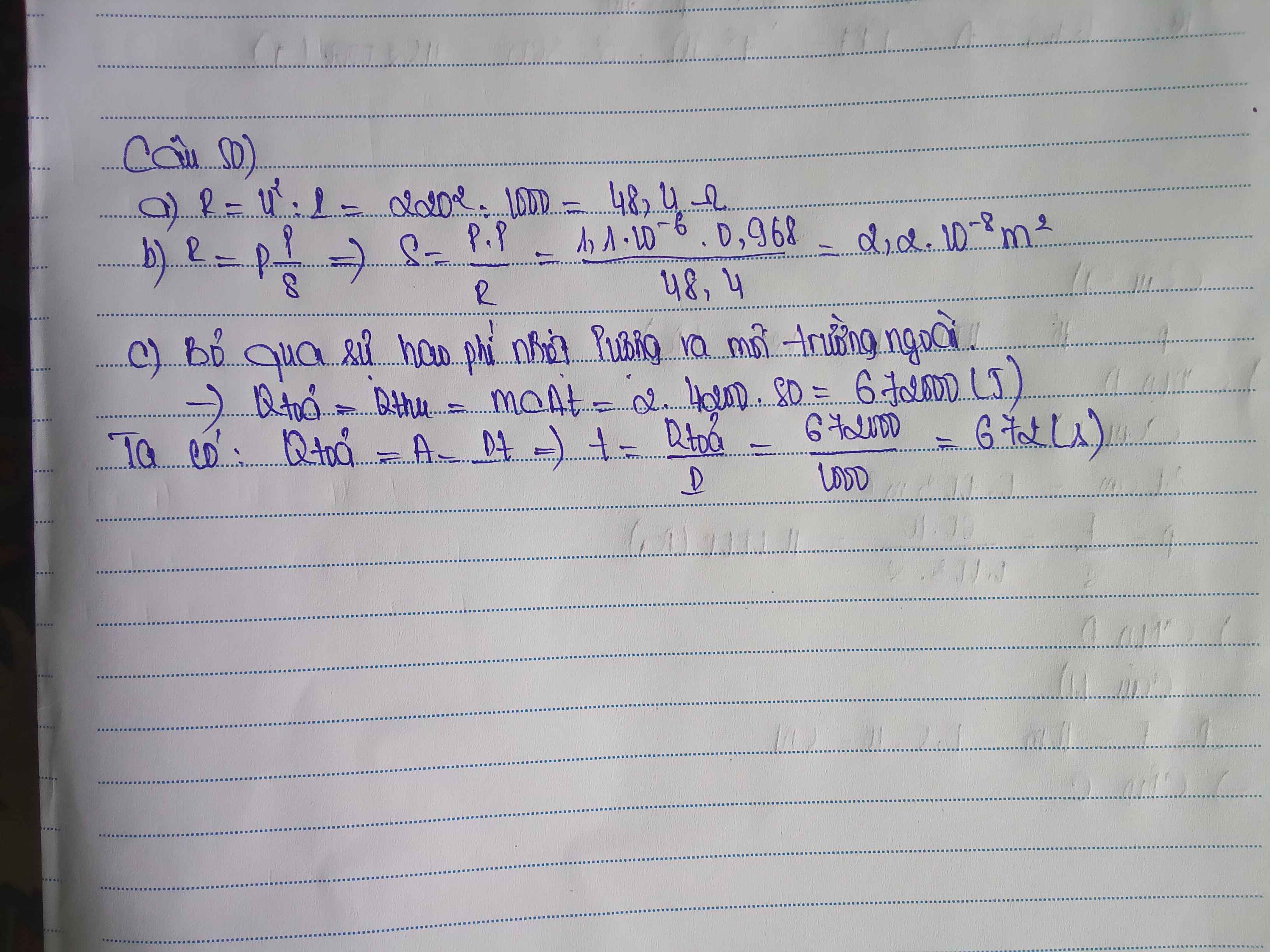
a. \(R=U^2:P=220^2:605=80\Omega\)
b. \(H=\dfrac{Q_{thu}}{Q_{toa}}100\%=\dfrac{mc\Delta t}{UIt}100\%=\dfrac{2\cdot4200\cdot75}{220\cdot\dfrac{605}{220}\cdot20\cdot60}100\%\approx86,7\%\)
a)Ta có:P=\(\dfrac{U^2}{R}\)⇒R=\(\dfrac{U^2}{P}\)=\(\dfrac{220^2}{605}\)=80(Ω)
b)H=\(\dfrac{Q_{ci}}{Q_{tp}}\).100%=\(\dfrac{mc\Delta t}{Pt}\)=\(\dfrac{2.4200.75}{605.20.60}\).100≃86,77%