plsssss hlep meeeeeeeeeee:

MP

My Phạm Trà

21 tháng 11 2021

plsssss hlep meeeeeeeeeee:<<<<<cho tam giác ABC có đường cao AD cắt đường cao BE tại H. Gọi M là trung điểm của đoạn thẳng BC. Trên tia HM lấy Q sao cho HM=MQ.a) Chứng minh tứ giác HCQB là hình bình hành.b) Chứng minh CQ vuông góc với AC và BQ vuông góc với AB.c) Trên tia HD lấy P sao cho HD=DP. Chứng minh DM là đường trung bình của tam giác PHQ từ đó chứng minh tứ giác BPQC là hình thang...

Đọc tiếp

#Toán lớp 8

0

KH

Khánh Hà

23 tháng 11 2021

giúp mình plsssss

#Tiếng anh lớp 7

1

H

htfziang

23 tháng 11 2021

bài viết dài thì bạn nên tự làm ấy, chứ cop nguyên của ngkh nó kì lắm

dùng trí tưởng tượng -> nghĩ ra cốt truyện -> dùng gg dịch hoặc cambridge dic -> xong bài :)))

Đúng(1)

TN

Trọng Nguyễn

21 tháng 10 2021

bai 13 plsssss

#Toán lớp 7

2

OY

OH-YEAH^^

21 tháng 10 2021

Bài 13

a) Ta có: OAt+AOy=180⁰

Mà hai góc này ở vị trí trong cùng phía

⇒ At//Oy

Đúng(0)

TN

Trọng Nguyễn

21 tháng 10 2021

câu b thì sao

Đúng(0)

DT

Đinh Trí Gia BInhf

19 tháng 6 2023

Help me plsssss

#Toán lớp 8

3

Y

YangSu

19 tháng 6 2023

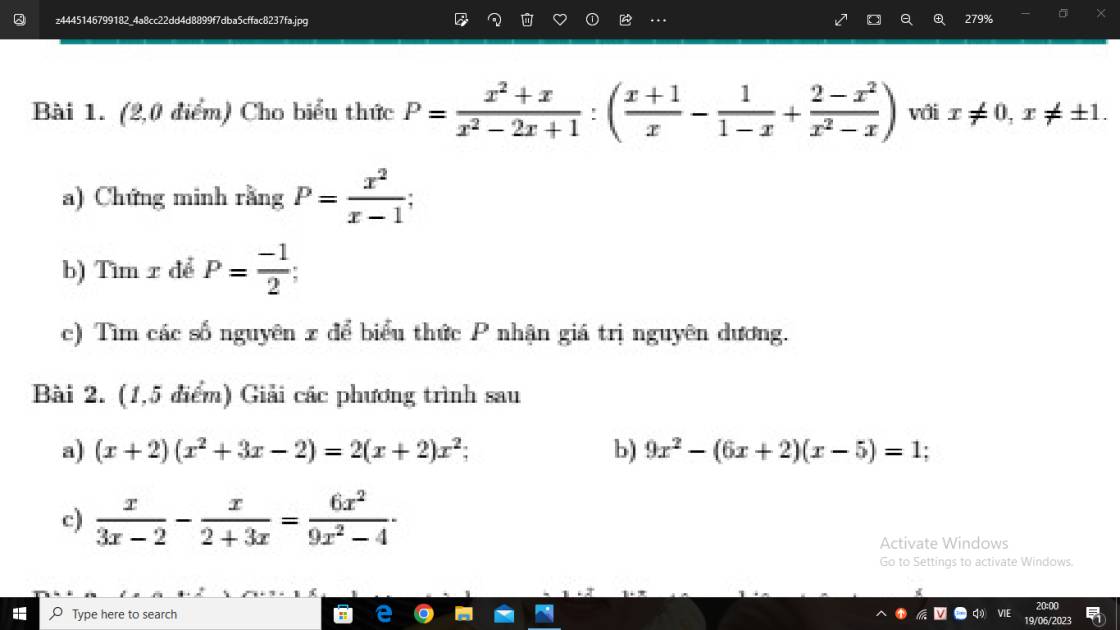
Bài 2 :

\(a,\left(x+2\right)\left(x^2+3x-2\right)=2\left(x+2\right)x^2\)

\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2\right)-2x^2\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x^2+3x-2-2x^2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\-x^2+3x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x^2+x+2x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\-x\left(x-1\right)+2\left(x-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left(x-1\right)\left(-x+2\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x-1=0\\-x+2=0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\end{matrix}\right.\)

Vậy \(S=\left\{-2;2;1\right\}\)

\(b,9x^2-\left(6x+2\right)\left(x-5\right)=1\)

\(\Leftrightarrow9x^2-\left(6x^2-30x+2x-10\right)-1=0\)

\(\Leftrightarrow9x^2-6x^2+30x-2x+10-1=0\)

\(\Leftrightarrow3x^2+28x+9=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-9\end{matrix}\right.\)

Vậy \(S=\left\{-\dfrac{1}{3};-9\right\}\)

\(c,\dfrac{x}{3x-2}-\dfrac{x}{2+3x}=\dfrac{6x^2}{9x^2-4}\left(dkxd:x\ne\pm\dfrac{2}{3}\right)\)

\(\Leftrightarrow\dfrac{x}{3x-2}-\dfrac{x}{3x+2}-\dfrac{6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)

\(\Leftrightarrow\dfrac{x\left(3x+2\right)-x\left(3x-2\right)-6x^2}{\left(3x-2\right)\left(3x+2\right)}=0\)

\(\Leftrightarrow3x^2+2x-3x^2+2x-6x^2=0\)

\(\Leftrightarrow4x-6x^2=0\)

\(\Leftrightarrow-2x\left(-2+3x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\-2+3x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=\dfrac{2}{3}\left(ktmdk\right)\end{matrix}\right.\)

Vậy \(S=\left\{0\right\}\)

Đúng(5)

Y

YangSu

19 tháng 6 2023

Bài 1 :

\(a,P=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\left(dkxd:x\ne0,x\ne\pm1\right)\)

\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)

\(=\dfrac{x^2+x}{\left(x-1\right)^2}:\left(\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\right)\)

\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}\)

\(=\dfrac{x^2}{x-1}\left(dpcm\right)\)

\(b,P=-\dfrac{1}{2}\Rightarrow\dfrac{x^2}{x-1}=-\dfrac{1}{2}\)

\(\Rightarrow2x^2=-\left(x-1\right)\)

\(\Rightarrow2x^2=-x+1\)

\(\Rightarrow2x^2+x-1=0\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)

Vậy \(P=-\dfrac{1}{2}\) thì \(x=\dfrac{1}{2};x=-1\)

\(c,\) Để P nhận giá trị nguyên dương thì \(P\ge0\)

\(\Leftrightarrow\dfrac{x^2}{x-1}\ge0\Leftrightarrow x\ge0\)

Đúng(3)

NH

Nguyễn Hoàng Diệp

8 tháng 12 2023 - olm

help meeeeeeeeeee

#Toán lớp 7

0

VB

Văn Bảo Nguyễn

4 tháng 3 2022

help me plsssss nowwwwwwwwwwwwwwwww

#Tiếng anh lớp 5

0

GN

Giúp nan ơi ( hải) hải giúp ?

4 tháng 4 2021

Nan ơi giúp plsssss

#Tiếng anh lớp 5

2

H

heliooo

4 tháng 4 2021

Sorry, mình không biết làm phần Task 1 nhaaa :<<<

Task 2: Complete the sentences using PAST SIMPLE TENSE.

1. didn't like

2. phoned

3. went

4. Did they leave

5. Did you like

6. didn't finish

7. Did she go

8. stayed / got

9. went

10. Did you travel

Chúc bạn học tốt!! ^^

Đúng(1)

GN

Giúp nan ơi ( hải) hải giúp ?

4 tháng 4 2021

thank

Đúng(0)

V

votuananh

3 tháng 11 2021

giúp mình vơi plsssss!

#Toán lớp 8

1

LL

Lấp La Lấp Lánh

3 tháng 11 2021

a) \(=3\left(xy-4\right)\)

b) \(=x^2\left(x-y\right)+4\left(x-y\right)=\left(x-y\right)\left(x^2+4\right)\)

c) \(=x^2-\left(y^2-12y+36\right)=x^2-\left(y-6\right)^2=\left(x-y+6\right)\left(x+y-6\right)\)

d) \(=\left(4p^2-36p+81\right)-25=\left(2p-9\right)^2-25=\left(2p-9-5\right)\left(2p-9+5\right)=4\left(p-7\right)\left(p-2\right)\)

Đúng(0)

V

votuananh

3 tháng 11 2021

giúp mình với plsssss!

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 11 2021

b: \(\Leftrightarrow x^2-4-x-x=0\)

hay x=-4

Đúng(0)

DL

Dieu Linh Dang

10 tháng 8 2021

giúp mk với ak, plsssss

#Tiếng anh lớp 6

1

DT

Đỗ Thanh Hải

CTVVIP

10 tháng 8 2021

1 saw - didn't see - was looking

2 met - went - went - had - were waiting

3 was cycling - stepped - was going - managed - didn't hit

4 was waiting - arrived

5 were you doing

6 Did you go

7 wore

8 were you driving - happened

9 took - wasn't looking

10 were - didn't know

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP