Question

[Pham Trong Bach]

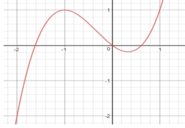
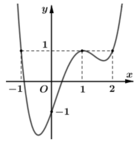
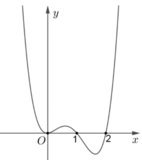
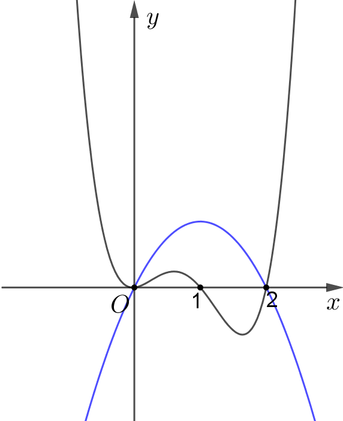
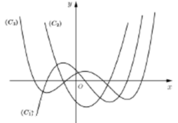
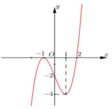
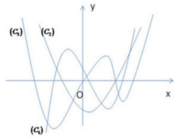
Cho hàm số y = f x  có đạo hàm liên tục trên R và đồ thị hàm số y = f ' x  là hình vẽ bên. Đặt g x = f x − x 2 2 . Điều kiện cần và đủ để đồ thị hàm số y = g x  cắt trục hoành tại 4 điểm phân biệt là

A. g 0 > 0 g 1 < 0

B.     g 0 > 0 g 1 < 0 g 1 . g − 2 > 0

C.  g 0 > 0 g − 2 > 0  

D.  g 0 > 0 g − 2 ≤ 0 g 1 ≤ 0  

Answer 1

[Cao Minh Tâm]

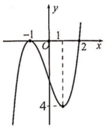
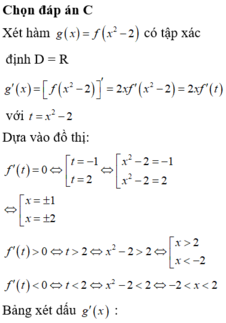
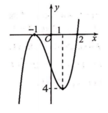
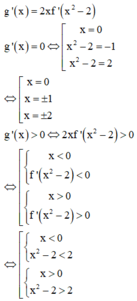
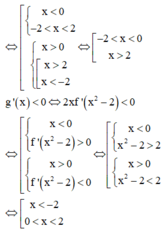
Đáp án B

Ta có   g x = f x − x 2 2 → g ' x = f ' x − x ;    ∀ x ∈ ℝ

Phương trình g ' x = 0 ⇔ f ' x = x . Dựa vào hình vẽ, ta thấy đồ thị hàm số y = f ' x  cắt đường thẳng y = x  tại ba điểm phân biệt   x = − 2 ;   x = 0 ;   x = 1

Do đó, để phương trình g x = 0  có 4 nghiệm phân biệt   ⇔ g 0 > 0 g 1 < 0 ,   g − 2 < 0