Cho đồ thị hàm số y = x 3 - 6 x 2 + 9 x - 2 như hình vẽ
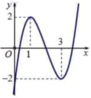
Khi đó phương trình | x 3 - 6 x 2 + 9 x - 2 | = m (m là tham số ) có 6 nghiệm phân biệt khi và chỉ khi
A. -2≤m≤2
B. 0<m<2
C. 0≤m≤2
D. -2<m<2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: 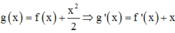
![]()
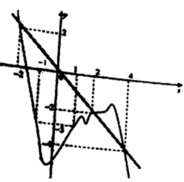
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
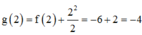
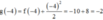
Bảng biến thiên:
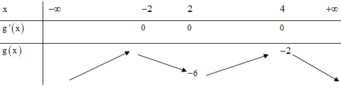
Dựa vào bảng biến thiên ta thấy ![]() => phương trình g(x) = 0 không có nghiệm
=> phương trình g(x) = 0 không có nghiệm ![]()

Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)

Đáp án B
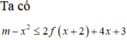
![]()
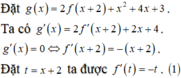
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
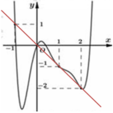
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có




Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)
Chọn B
+ Đồ thị hàm số y = | x 3 - 6 x 2 + 9 x - 2 | có được bằng cách biến đổi đồ thị (C) hàm số y = x 3 - 6 x 2 + 9 x - 2
Giữ nguyên phần đồ thị (C) nằm trên trục hoành.
Lấy đồi xứng phần đồ thị của (C) phần dưới trục hoành qua trục hoành.
Xóa phần đồ thị còn lại (C) phía dưới trục hoành.
+ Số nghiệm của phương trình | x 3 - 6 x 2 + 9 x - 2 | = m là số giao điểm của đồ thị hàm số
y = | x 3 - 6 x 2 + 9 x - 2 | và đồ thị hàm số y=m. Để phương trình có 6 nghiệm phân biệt thì điều kiện cần và đủ là 0<m<2.