Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án A
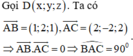
Do đó bốn diểm A, B, C, D lập thành một hình chữ nhật
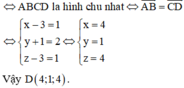
Đáp án là C.
Toạ độ trọng tâm của tứ diện A B C D :
x = x A + x B + x C + x D 4 = 2 y = y A + y B + y C + y D 4 = 3 z = z A + z B + z C + z D 4 = 1
Chọn đáp án C
Ta có A B ⇀ = 0 ; 2 ; - 1 , A C ⇀ = - 1 ; 1 ; 2 và A D ⇀ = - 1 ; m + 2 ; p .
Suy ra A B ⇀ , A C ⇀ = 5 ; 1 ; 2
⇒ A B ⇀ , A C ⇀ . A D ⇀ = m + 2 p - 3
Để bốn điểm A, B, C, D đồng phẳng thì A B ⇀ , A C ⇀ . A D ⇀
⇔ m + 2 p = 3
Phương trình mặt phẳng (ABC): x+y+z-1=0
Phương trình mặt phẳng (BCD): x=0
Phương trình mặt phẳng (CDA): y=0
Phương trình mặt phẳng (ĐBA): z=0
Gọi I(x;y;z) là điểm cách đều bốn mặt phẳng (ABC),(BCD),(CDA),(DBA)
⇒ x + y + z - 1 3 = x = y = z
TH1: x = y = z ⇒ 3 x - 1 3 = x
⇔ [ x = 1 3 + 3 x = 1 3 - 3 ⇒ I 1 3 + 3 ; 1 3 + 3 ; 1 3 + 3
hoặc I 1 3 - 3 ; 1 3 - 3 ; 1 3 - 3
TH2: - x = y = z ⇒ - x - 1 3 = x
⇔ [ x = 1 3 - 1 x = - 1 3 + 1 ⇒ I 1 3 - 1 ; - 1 3 - 1 ; - 1 3 - 1
hoặc I - 1 3 + 1 ; 1 3 + 1 ; 1 3 + 1
TH3: x = y = - z ⇒ x - 1 3 = x
hoặc I 1 3 - 1 ; - 1 3 - 1 ; 1 3 - 1
TH4: x = y = - z ⇒ x - 1 3 = x
⇔ [ x = - 1 3 - 1 x = 1 3 + 1 ⇒ I - 1 3 - 1 ; - 1 3 - 1 ; 1 3 - 1
hoặc I 1 3 + 1 ; 1 3 + 1 ; - 1 3 + 1
Vậy, có tất cả 8 điểm thỏa mãn.
Chọn đáp án C.
Đáp án A
A B → = − 1 ; 3 ; − 1 , A C → = 2 ; 1 ; 0 ⇒ n → = 1 ; − 2 ; − 7 .
Phương trình mặt phẳng A B C : x + 1 − 2 y − 7 z − 1 = x − 2 y − 7 z + 8 = 0
Gọi H là hình chiếu của D lên mặt phẳng (ABC) ta có
D H : x = 2 + t y = 1 − 2 t z = 1 − 7 t
Ta tìm tọa độ điểm H
2 + t − 2 1 − 2 t − 7 1 − 7 t + 8 = 0 ↔ 54 t = − 1 ⇒ t = − 1 54 .
Vậy H 107 54 ; 28 27 ; 61 54 .
Đáp án A
⇒ A B → , A C → , A D → đồng phẳng suy ra tồn tại vô số mặt phẳng cách đều 4 điểm trên