Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C chia cung lớn AB thành hai cung AC và CB .chứng minh rằng cung lớn AB có sđ ∠ AB = sđ ∠ AC + sđ ∠ CB
Hướng dẫn: Xét ba trường hợp:
Tia OC nằm trong góc đối đỉnh của góc ở tâm AOB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 11 2019
Trường hợp tia OC nằm trong một góc kề bù với góc ở tâm AOB. Kẻ đường kính AE
CM
22 tháng 3 2018
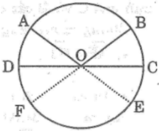
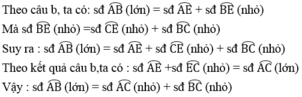
Trường hợp tia OC trùng với tia đối của một cạnh của góc ở tâm AOB (hình b)
CM
15 tháng 3 2018
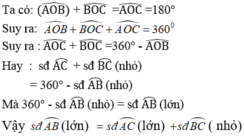
* Trường hợp 1 . Điểm C nằm trên cung lớn AB.
Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.
Do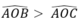 
nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
Suy ra: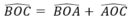 
= 1000+ 450 = 1450
Khi đó, số đo cung nhỏ BC là 1450 ( bằng góc ở tâm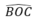 
)
Số đo cung lớn BC là: 3600 - 1450 = 2150
* Trường hợp 2: Điểm C nằm trên cung nhỏ AB
Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB
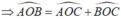
Ta có: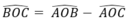 
= 1000- 450 = 550
Khi đó, số đo cung nhỏ BC là 550
Số đo cung lớn BC là: 3600- 550 = 3050
11 tháng 4 2017
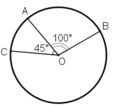
a) Điểm C nằm trên cung nhỏ AB ( hình a)
Số đo cung nhỏ BC = 100º – 45º = 55º
Số đo cung lớn BC = 360º – 55º = 305º
b) Điểm C nằm trên cung lớn AB (hình b)
Số đo cung nhỏ BC = 100º + 45º = 145º
Số đo cung lớn BC = 360º – 145º = 215º
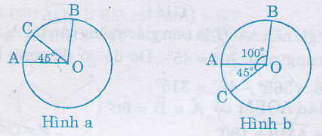
Trường hợp tia OC nằm trong góc đối đỉnh của góc ở tâm AOB (hình a).
Kẻ đường kính CD. Ta có :