Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm. Tính độ dài dây ngắn nhất đi qua M.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


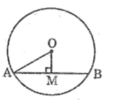
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)
a. Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (\(\frac{1}{2}\)).AB
Hay: AB = 2AM = 2.4 = 8 (dm)
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O). Vậy dây có độ dài bằng 2R = 2.5 = 10 (dm)

O M M' A B
a) Giả sử dây AB bất kì đi qua M. Ta kẻ \(OM'\perp AB\) (M' thuộc AB)
Xét trong tam giác OMM' , ta có : \(OM\ge OM'\)(quan hệ giữa đường xiên và hình chiếu)
Do đó : dây AB dài nhất \(\Leftrightarrow AB\perp OM\)
Vậy dây ngắn nhất vuông góc với bán kính đi qua M
Tới đây áp dụng đ/l Pytago là ra...
b) Dây dài nhất là dây đi qua tâm...
O A M B
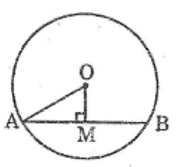
a) Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có :
OA2 = AM2 + OM2
Suy ra: AM2 = OA2 – OM2 = 52 – 32 = 16
AM = 4 ( dm )
Ta có: \(OM\perp AB\)
Suy ra: \(AM=\left(\frac{1}{2}\right).AB\)
Hay: AB = 2AM = 2 . 4 = 8 ( dm )
b. Dây đi qua M lớn nhất khi nó là đường kính của đường tròn (O)
Vậy dây có độ dài bằng
2R = 2 . 5 = 10 ( dm )

Gọi dây đi qua M là AB. Kẻ OH vuông góc AB tại H.
Có MB AB≤2R=10
và OM≥OHOM≥OH quan hệ đường vuông góc và đường xiên.
vậy OH có giá trị lớn nhất bằng OM, khi đó độ dài dây AB nhỏ nhất = 8dm (liên hệ dây cung và khoảng cách đến tâm)
....... Từ đó suy ra kết quả.
a) Dây ngắn nhất đi qua M chính là dây vuông góc với bán kính.
Sau đó áp dụng đl Pytago là ra.
b) Dây dài nhất đi qua M chính là đường kính.

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

Dây đi qua M ngắn nhất là dây AB vuông góc với OM
Áp dụng định lí Pitago vào tam giác vuông OAM ta có:
O A 2 = A M 2 + O M 2
Suy ra: A M 2 = O A 2 - O M 2 = 5 2 - 3 2 = 16
AM = 4 (dm)
Ta có: OM ⊥ AB
Suy ra: AM = (1/2).AB
Hay: AB = 2AM = 2.4 = 8 (dm)