Hình nón có đỉnh là tâm mặt cầu (S) góc ở đỉnh hình nón bằng 120 o đường tròn đáy hình nón thuộc mặt cầu (S) Tính tỷ số k = V N V C ( V N , V C là thể tích hình nón và hình cầu kể trên).
![]()
![]()
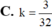
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

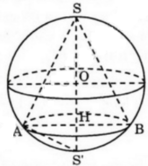
Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.


Chọn đáp án A.
Góc ở đỉnh hình nón là φ = 120 ° là góc tạo bởi khi mặt phẳng đi qua trục SO => O S C ^ = 60 °
Khi cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Xét tam giác vuông SOC tại O:
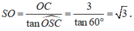
Xét tam giác vuông SOA tại O:
![]()
Do tam giác SAB đều:
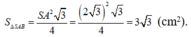

Đáp án A.
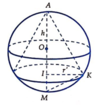
Kí hiệu như hình vẽ.
Ta thấy I K = r ' là bán kính đáy của hình chóp, A I = h là chiều cao của hình chóp.
Tam giác vuông tại K có IK là đường cao
⇒ I K 2 = A I . I M ⇒ r ' 2 = h . 2 r − h
Ta có V c o h p = 1 3 . π r ' 2 . h = 1 3 . π . h . h . 2 r − h = 4 3 π . h 2 . h 2 2 r − h .
Áp dụng bất đẳng thức Cauchy ta có
h 2 . h 2 . 2 r − h ≤ h 2 + h 2 + 2 r − h 3 27 = 8 r 3 27
⇔ V c h o p ≤ 4 3 π . 8 r 3 27 = 32 81 . π r 3
Dấu bằng xảy ra khi h 2 = 2 r − h ⇔ h = 4 r 3 . Vậy ta chọn A
Chọn C