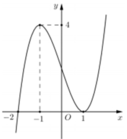
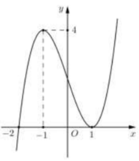
Cho hàm số y = f(x) có đạo hàm trên M và không có cực trị, đồ thị của hàm số y = f(x) là đường cong ở hình vẽ bên. Xét hàm số h x = 1 2 f x 2 - 2 x f x + 2 x 2 . Mệnh đề nào sau đây đúng?
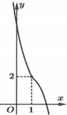
A. Đồ thị hàm số y = h(x) có điểm cực tiểu là M (1;0).
B. Hàm số y = h(x) không có cực trị.
C. Đồ thị của hàm số y = h(x) có điểm cực đại là N(1;2).
D. Đồ thị hàm số y = h(x) có điểm cực đại là M (1;0).

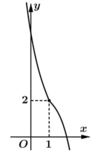
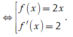
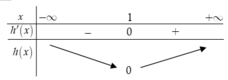

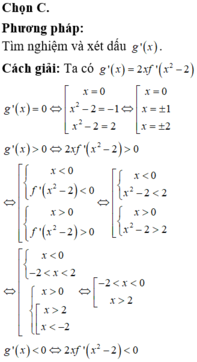

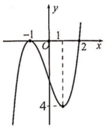
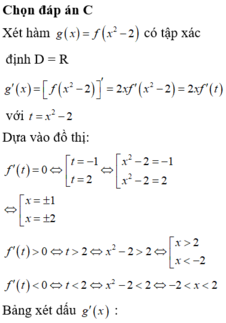


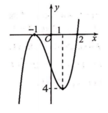
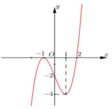
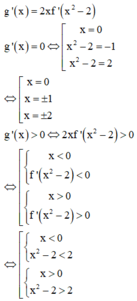
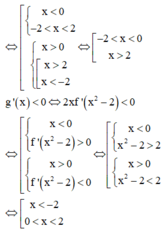

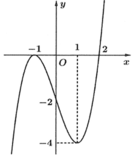

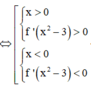
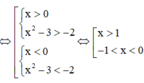
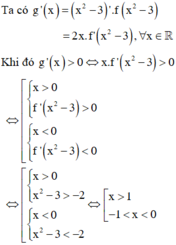
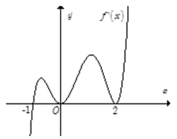
Chọn đáp án A.