Cho F x = − 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f '(x).lnx
A. ∫ f ' x lnxdx = lnx x 3 + 1 5 x 5 + C .
B. ∫ f ' x lnxdx = lnx x 3 − 1 5 x 5 + C .
C. ∫ f ' x lnxdx = lnx x 3 + 1 3 x 3 + C .
D. ∫ f ' x lnxdx = − lnx x 3 + 1 3 x 3 + C .

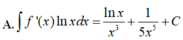
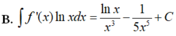
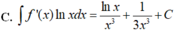
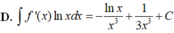

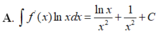
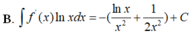
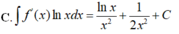
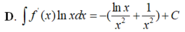
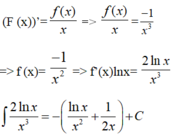
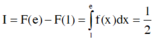
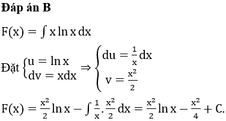
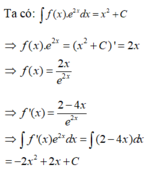
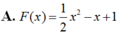
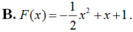
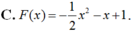
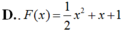
Đáp án C
F x = − 1 3 x 3 là một nguyên hàm của f x x nên
Áp dụng công thức nguyên hàm từng phần ta có
∫ f ' x lnxdx = ∫ lnxd f x = lnx . f x − ∫ f x x dx = lnx x 3 + 1 3 x 3 + C