Cho hàm số y = f x = x 4 + a x 3 + b x 2 + c x + 4 (C). Biết đồ thị hàm số cắt trục hoành tại ít nhất 1 điểm. Tìm giá trị nhỏ nhất của biểu thức T = 20 a 2 + 20 b 2 + 5 c 2 .
A. 32
B. 64
C. 16
D. 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 12 2019
Đáp án D
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có
CM
27 tháng 9 2018
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
CM
2 tháng 6 2018
Đáp án B.
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:
Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.
CM
6 tháng 3 2017
Đáp án là D
Từ đồ thị f ’(x) ta lập được BBT của f(x)
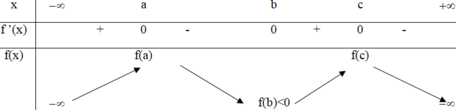
=> Có 4 nghiệm là nhiều nhất
CM
28 tháng 3 2018
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
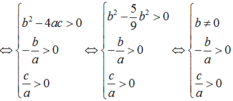
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
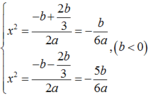
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
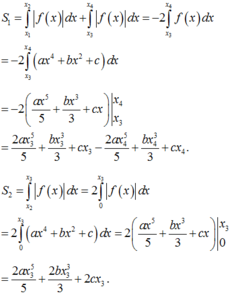
Suy ra
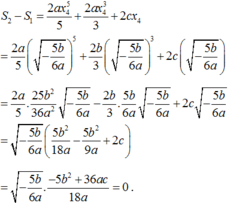
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
CM
22 tháng 6 2017
Ta có bảng biến thiên như hình vẽ bên.
Vì f( b) < 0 nên rõ ràng có nhiều nhất 2 giao điểm.
Chọn B.
20 tháng 12 2022
a: Để (d)//Ox thì m-1=0
=>m=1
b: Thay x=-1 và y=1 vào (d), ta được:
-m+1+m=1
=>1=1(luôn đúng)
c: Thay x=\(\dfrac{2-\sqrt{3}}{2}\) và y=0 vào (d), ta đc:
\(\left(m-1\right)\cdot\dfrac{2-\sqrt{3}}{2}+m=0\)
=>\(\left(m-1\right)\cdot\left(2-\sqrt{3}\right)+2m=0\)
=>\(2m-\sqrt{3}m-2+\sqrt{3}+2m=0\)
=>\(m\left(4-\sqrt{3}\right)=2-\sqrt{3}\)
=>\(m=\dfrac{2-\sqrt{3}}{4-\sqrt{3}}\)
Đáp án B
Dựa vào đồ thị hàm số