Cho cấp số nhân ( u n ) có u n = 2 ( - 3 ) n + 1 . Tìm công bội q của cấp số nhân đó
A. q = 6 ( 3 + 1 )
B. q = - 6 ( 3 + 1 )
C. q = 3
D. q = - 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
30 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
HT
19 tháng 1 2021
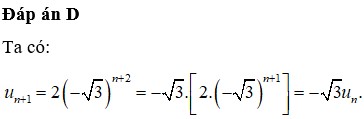
\(S_1=u_1=4-2=2\)
\(S_2=u_1+u_2=4^2-2.2=12\Rightarrow u_2=12-2=10\)
\(\Rightarrow q=\dfrac{u_2}{u_1}=\dfrac{10}{2}=5\)
AH
Akai Haruma
Giáo viên
13 tháng 10 2023
1. Gọi công bội của csn đó là $q$ thì:
$u_6=q^4u_2$
$\Leftrightarrow 32=q^4.2\Leftrightarrow q^4=16$
$\Leftrightarrow q=\pm 2$
2.
$u_{2019}=q^{2018}u_1=2.3^{2018}$
