Kí hiệu F(x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F(0) = -ln2. Tìm tập nghiệm S của phương trình
A. S = {-3;3}
B. S = {3}
C. S = ∅
D. S = {-3}
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3

Ta có ![]()
![]()
Quan sát đồ thị có 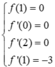
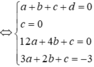

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 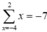
Chọn đáp án C.

Chọn D
Đặt t = 8 - x 2 ⇒ t 2 = 8 - x 2 ⇒ - t d t = x d x
∫ x 8 - x 2 d x = - ∫ t d t t = - t + C = - 8 - x 2 + C
Vì F ( 2 ) = 0 nên - 8 - 4 + C = 0 suy ra C = 2.
Ta có phương trình - 8 - x 2 + 2 = x ⇔ x = 1 - 3

Chọn C.
Vì: f’(x) = 15(x + 1)2 + 4 ;
f”(x) = 30(x + 1) ⇔ f”(x) = 0 ⇔ x = -1.
Đáp án B.