Cho hình chóp S.ABC có mp(SAB) ⊥ mp(ABC), tam giác ABC đều cạnh 2a, tam giác SAB vuông cân tại S. Tính thể tích hình chóp SABC
A. a 3 3 3
B. a 3 3 6
C. 2 a 3 3 3
D. a 3 3 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Vì tam giác SAB cân tại S nên hạ SH ⊥ AB => H là trung điểm của AB.
Vì 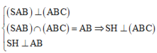
Tam giác SAB vuông cân tại S nên SA = SB = a 2
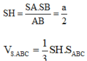
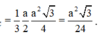

Gọi M là trung điểm cạnh AB
Dựa vào tính chất hai mặt phẳng vuông góc với nhau suy ra SM⊥(ABC)
⇒ V S.ABC = 1/3.SΔABC.SM = 1/3.1/2.AC.BC.SM
Gọi N là trung điểm của đoạn AC
MN là đường trung bình của tam giác ABC
⇒ MN ⊥ AC; MN = 1/2.BC = a
Chỉ ra góc giữa mặt phẳng (ABC) và mặt phẳng (SAC) là SMN=60 độ
Tính thể tích hình chóp S.ABC
SM = MN.tanSNM = a.tan60 = a√3.
SN = MN/cosSNM = a/cos60 = 2a.
AB = 2SM = 2a√3.
AC = √(AB^2 − BC^2) = √[(2a√3)^2−(2a)^2]=2a√2
Vậy V S.ABC = 1/3.SΔABC.SM = 1/3.1/2.AC.BC.SM = (2a^3√6)/3 (đvtt)

chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)
Đáp án là A
Ta có :
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là
Vậy thể tích khối chóp SABC là: