Một vật có khối lượng bằng 40 g, dao động với chu kỳ T và có biên độ 13 cm. Khi vật có vận tốc bằng 25 cm/s thì thế năng của nó bằng 7 , 2 . 10 − 3 J . Chu kì T bằng
A. 0,4πs
B. 1,2s
C. 2,4π s
D. 0,5πs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
W t = W − W d = 1 2 m 2 π T 2 A 2 − v 2 2 π T 2 ⇔ 7 , 2.10 − 3 = 1 2 .40.10 − 3 . 2 π T 2 0 , 13 2 − 0 , 25 2 2 π T 2 ⇔ T = 0 , 4 π s

\(v=\omega\sqrt{A^2-x^2}=\dfrac{2\pi}{T}\sqrt{A^2-x^2}=5\pi\sqrt{3}\left(cm.s^{-1}\right)\)

Đáp án D
+ Tần số góc của dao động
ω = 2 π T = 2 π 2 = π r a d / s
→ Tốc độ của vật tại vị trí có li độ x : v = ω A 2 - x 2 = π 10 2 - 6 2 ≈ 25 , 13 c m / s

Đáp án B
Phương pháp: Áp dụng hệ thức độc lập với thời gian của vận tốc và li độ
Cách giải:
Tần số góc: ω = 2π/T = π (rad/s)
Tốc độ của vật khi cách VTCB 6cm:
![]()
![]()
=> Chọn B

Đáp án A
Chu kì dao động của vật không phụ thuộc vào biên độ nên nếu kích thích cho vật dao động với biên độ bằng 6 cm thì chu kì dao động của vật vẫn là T = 0,3 s
Chu kì dao động của động năng: T' = T 2 = 0 , 3 2 = 0 , 15 s

Chọn A
+ Động năng và thế năng biến thiên với ω' = 2ω => T' = T/2
+ Thay (x1 = 4cm; v1 =40π√3 cm/s) và (x2 = 4√2 cm; v2 = 40π√2 cm/s) vào 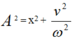 .ta được hệ phương trình hai ẩn A2 và
.ta được hệ phương trình hai ẩn A2 và ![]()
Giải hệ phương trình ta được ω = 10π rad/s => T = 0,2s => T' = 0,1 (s).
Đáp án A