Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
=
2
x
4
+
2
m
x
2
−
3
m
2
có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S. A.
2
−
2
3
. B.
−
2
−
...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 4 + 2 m x 2 − 3 m 2 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
A. 2 − 2 3 .
B. − 2 − 3 .
C. -1.
D. 0.
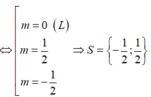
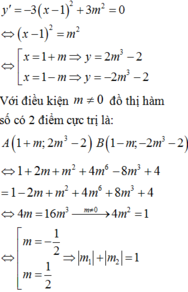
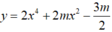có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.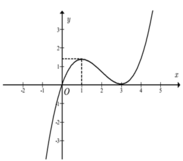
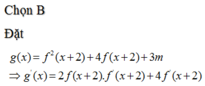
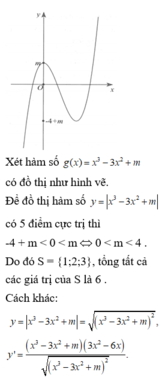
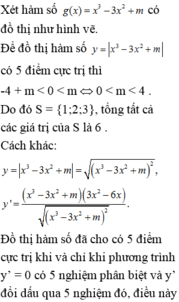
Đáp án B
Đồ thị hàm số có 3 điểm cực trị ⇔ y ' = 4 x 2 x 2 + m đổi dấu 3 lần ⇔ m < 0
Khi đó, gọi A 0 ; − 3 m 2 , B − m 2 ; − m 2 − 3 m 2 và C − − m 2 ; − m 2 − 3 m 2 là 3 điểm cực trị
Vì y A > y B = y C nên yêu cầu bài toán
<=> Tứ giác ABOC nội tiếp (I)
Vì A B = A C O B = O C → O A là đường trung trực của đoạn thẳng BC
Suy ra OA là đường kính của (I)
=> I ⇒ O B → . A B → = 0 ⇔ − m 2 + m 2 2 . m 2 + 3 m 2 = 0 ⇔ m = − 1 m = − 1 − 3
Vậy tổng các giá trị của tham số m là − 2 − 3