Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
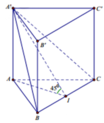
Gọi I là trung điểm của BC. Đặt A ' A = x ⇒ A I = x , A ' I = x 2
Khi đó: B C = 2 B I = 2. A I tan 30 ° = 2 x 3 S A ' B C = 1 2 A I ' . B C = a 2 6 ⇔ 1 2 x 2 . 2 x 3 = a 2 6 ⇔ x = a 3 ⇒ B C = 2 x 3 = 2 a 3 3 = 2 a
Bán kính mặt đáy hình trụ ngoại tiếp hình lăng trụ là R = 2 a 3 4 a 2 3 = 2 a 3
Diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ là S x q = 2 π . 2 a 3 . a 3 = 4 π a 2
Đáp án là C
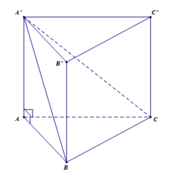
+) Ta có tam giác ABC là hình chiếu vuông góc của tam giác A'BC trên mặt phẳn (ABC)
+) Gọi φ là góc giữa (A'BC) và (ABC).
Ta có :
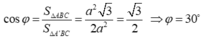
Đáp án là A
Gọi là trung M điểm của BC
Chứng minh được BC ⊥ (AA'M) . Do đó góc giữa hai mặt phẳng (A'BC) và mặt phẳng (ABC) là góc A ' M A ^ = 30 o
Đặt AB = x
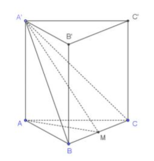
Tam giác là hình ABC chiếu của tam giác A'BC lên mặt phẳng (ABC)
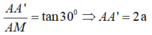
Chọn A.
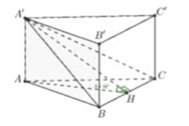
Gọi H là trung điểm của BC
Đặt AB = a ta có: AH = a 3 2
Xét tam giác A'AH ta tìm được: A'H= a, AA'= a 2
S A ' B C = 8 ⇔ 1 2 A ' H . B C = 8 ⇔ a = 4
Thể tích của khối lăng trụ ABC.A'B'C' :
V = A A ' . S A B C = 8 3
Đáp án đúng : C