Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị như hình bên.
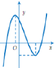
Khẳng định nào sau đây đúng?
A. a , d > 0 ; b , c < 0
B. a , b , d > 0 ; c < 0
C. a , c , d > 0 ; b < 0
D. a , b , c < 0 ; b , d > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số có tiệm cận đứng x = a > 0; tiệm cận ngang y = b > 0
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
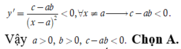

Chọn C
Ta có: ![]()
Dựa vào đồ thị:
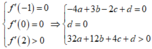

![]()
Dựa vào đồ thị, ta cũng có: ![]()
Từ (1),(2) suy ra a + c > 4a + c > 0.

Chọn đáp án A
Phương pháp
+) Quan sát đồ thị hàm số đã cho, và các đáp án trong đề bài, chọn ra câu đúng.
+) x = x 0 là điểm cực trị của hàm số y=f(x) => f ’ ( x 0 ) = 0 .
+) Số điểm cực trị của đồ thị hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0
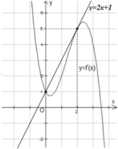
Cách giải
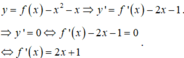
Số nghiệm của phương trình f’(x)=2x+1 là số giao điểm của đồ thị hàm số y=f’(x) và y=2x+1.
Dựa vào đồ thị hàm số ta thấy phương trình f’(x)=2x+1 có 2 nghiệm x=0 và x=2, tuy nhiên chỉ qua nghiệm x=0 thì y’ đổi dấu, do đó hàm số có 1 cực trị x=0

Chọn C
Dựa vào đồ thị của hàm số y= f’(x) ta thấy:
+ f’(x) > 0 khi x ∈ (-2;1) ∪ (1; + ∞)
=> Hàm số y= f(x) đồng biến trên các khoảng ( -2; 1) và ( 1; + ∞).
Suy ra A đúng, B đúng.
+ Ta thấy : f’(x)< 0 khi x< -2 ( chú ý nhận dạng đồ thị của hàm số bậc ba)
=> Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; -2) .
Suy ra D đúng.
+ Dùng phương pháp loại trừ, ta chọn C
Đáp án A
Phương pháp:
Quan sát đồ thị và nhận xét.
Cách giải:
Ta có hàm số: y = a x 2 + b x 2 + c x + d
Từ chiều biến thiên của đồ thị ta có a > 0.
Có: y 0 = d > 0
Đồ thị hàm số có hai điểm cực trị
=> phương trình: y = 3 a x 2 + 2 b x + c = 0 có hai nghiệm phân biệt x 1 và x 2 . Chọn x 1 < x 2
Mà x 1 < 0 < x 2 ⇒ a c < 0 ⇔ c < 0
Từ đồ thị ta có: x 1 − 0 < x 2 − 0 ⇒ a + b < 0 ⇔ b < − a < 0
Vậy: a , d > 0 ; b , c < 0