Môđun của số phức z=(-4+3i)i bằng:
A. 7
B.5
C.3
D.4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
PT
1
CM
30 tháng 9 2019
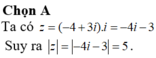
Đặt z = a + bi(a, b ∈ R). Ta có
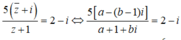
⇔ 5a - 5(b - 1)i = (2 - i)(a + 1 + bi)
⇔ 3a - b - 2 + (a - 7b + 6)i = 0
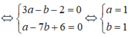
Suy ra z = 1 + i và w = 1 + ( 1 + i ) + ( 1 + i ) 2 = 2 + 3 i .
Vậy: | w | = ( 4 + 9 ) = 13
Chọn B
CM
2 tháng 11 2017
Đặt z = a + bi(a, b ∈ R). Ta có :
(1 + i)(z - i) = (1 + i)[a + (b - 1)i] = a - b + 1 + (a + b - 1)i
Từ giả thiết ta có: (1 + i)(z - 1) + 2z = 2i
⇔ a - b + 1 + (a + b - 1)i + 2(a + bi) = 2i ⇔ (3a - b + 1) + (a + 3b - 1)i = 2i
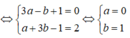
Suy ra z = 1 và
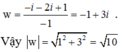
Chọn C
