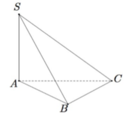
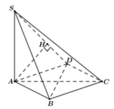
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Biết rằng AB = a , AC = a 3 và S A B ⏞ = 60 ° . Gọi H là hình chiếu vuông góc của A trên cạnh SC. Tính tỷ số thể tích của hai khối SABH và HABC.
A. 3 4
B. 1 12
C. 3 2
D. 7 4



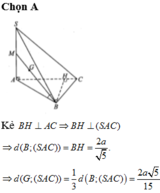

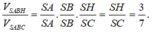
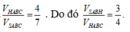
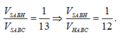
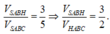
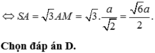
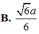
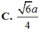
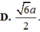


Đáp án A
Ta có S A = A B tan S B A = a 3 ; A C = A B 2 + B C 2 = 2 a .
Tam giác SAC vuông tại A có đường cao AH nên S C = S A 2 + A C 2 = a 7 và S H . S C = S A 2 .
Do đó S H S C = S A 2 S C 2 = 3 7 .
Mặt khác V S . A B H V S . A B C = S A S A . S B S B . S H S C = S H S C = 3 7
Suy ra V H A B C V S . A B C = 4 7 . Do đó V S . A B H V H A B C = 3 4