Cho D giới hạn bởi y=0,y=
x
3
-
4
x
2
+
x
+
6
thì diện tích D được tính bởi: ...
Đọc tiếp
Cho D giới hạn bởi y=0,y= x 3 - 4 x 2 + x + 6 thì diện tích D được tính bởi:
K
Khách
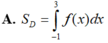
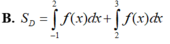
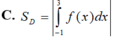
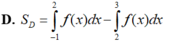
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
AH
Akai Haruma
Giáo viên
23 tháng 2 2021
Lời giải:
Trước tiên ta tìm giao điểm của 2 ĐTHS:
PT hoành độ giao điểm: $|x^2-4x+3|=x+3$
$\Rightarrow x=0$ hoặc $x=5$
Diện tích hình phẳng giới hạn bởi $(C)$ và $(d)$ là:
\(\int ^5_0(x+3-|x^2-4x+3|)dx=\frac{109}{6}\) (đơn vị diện tích)
AH
Akai Haruma
Giáo viên
10 tháng 10 2021
1.
\(V=\pi \int ^4_1[x^{\frac{1}{2}}e^{\frac{x}{2}}]^2dx=\pi \int ^4_1(xe^x)dx\)
\(=\pi \int ^4_1xd(e^x)=\pi (|^4_1xe^x-\int ^4_1e^xdx)\)
\(=\pi |^4_1(xe^x-e^x)=\pi (3e^4)=3\pi e^4\)
AH
Akai Haruma
Giáo viên
10 tháng 10 2021
2.
\(V=\pi \int ^1_0(x\sqrt{\ln (x^3+1)})^2dx=\pi \int ^1_0x^2\ln (x^3+1)dx\)
\(=\frac{1}{3}\pi \int ^1_0\ln (x^3+1)d(x^3+1)\)
\(=\frac{1}{3}\pi \int ^2_1ln tdt=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1td(\ln t))\)
\(=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1dt)=\frac{1}{3}\pi |^2_1(t\ln t-t)=\frac{1}{3}\pi (2\ln 2-1)\)
Đáp án D.