Hàm số y = f x liên tục trên ℝ và có bảng biến thiên như hình bên dưới.
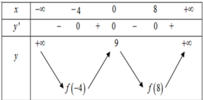
Biết f - 4 > f 8 , khi đó giá trị nhỏ nhất của hàm số đã cho trên ℝ bằng
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D.
Dựa vào bảng biến thiên suy ra hàm số nghịch biến trên (0;1)

Chọn đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên (a;b) có y’>0 với x thuộc (a;b) thì hàm số đồng biến trên (a;b).
Cách giải
Từ BBT ta có hàm số đồng biến trên các khoảng (-∞;-1) và (0;1).

Chọn C
Xét hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2]
![]()
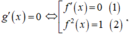
Từ bảng biến thiên, ta có:
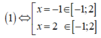
Và ![]() nên f(x) đồng biến trên [-1;2]
nên f(x) đồng biến trên [-1;2]
![]()
![]() nên (2) vô nghiệm
nên (2) vô nghiệm
Do đó, g'(x) = 0 chỉ có nghiệm là x = -1 và x = 2
Ta có ![]()
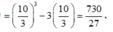
![]()
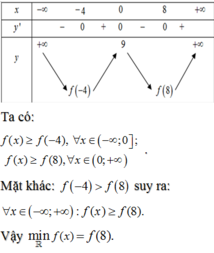
Vậy ![]()

Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.

Chọn C
Giá trị lớn nhất của hàm số f(x) trên [-3;2], ta có:
M = 2, m = -4 suy ra M - m = 6

Hàm số nghịch biến nếu f’(x)<0 Quan sát đồ thị y=f’(x), chọn đáp án A. Chọn A