Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu số tự nhiên của tham số m để phương phương trình: x 2 + y 2 + z 2 + 2 m − 2 y − 2 m + 3 z + 3 m 2 + 7 = 0 là phương trình của một mặt cầu.
A. 2
B. 3
C. 4
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C.
Để phương trình đã cho là phương trình mặt cầu thì
![]()
![]()

Chọn đáp án C.
Ta có
![]()
Phương trình x 2 + y 2 + z 2 + 2 m - 2 y - 2 m + 3 z + 3 m 2 + 7 = 0
là phương trình của một mặt cầu khi a 2 + b 2 + c 2 - d > 0
![]()
![]()
![]()
Do m ∈ N nên m ∈ 0 ; 1 ; 2 ; 3
Vậy có 4 giá trị m ∈ N thỏa mãn bài toán

Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8

Đáp án B.
Để phương trình x 2 + y 2 + z 2 - 4 x + 2 m y + 6 z + 13 = 0 là phương trình của mặt cầu thì
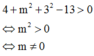
Đáp án là C.
+ Để phương trình đã cho là phương trình mặt cầu thì:
R = − m 2 + 2 m + 6 > 0 ⇔ 1 − 7 < m < 1 + 7 ;
mà m ∈ ℕ ⇒ m ∈ 0 ; 1 ; 2 ; 3 .