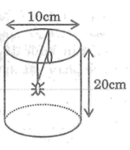
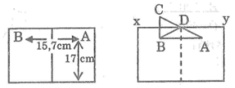
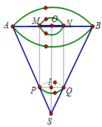
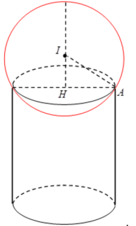
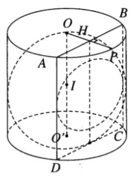
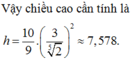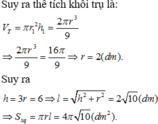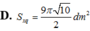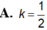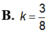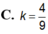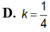Một lọ trống miệng đựng nước là hình trụ tròn xoay có chiều cao bằng 1,6dm; đường kính đáy bằng 1dm; đáy (dưới) của lọ phẳng với bề dày không đổi bằng 0,2dm; thành lọ với bề dày không đổi bằng 0,2dm; thiết diện qua trục của lọ như hình vẽ; đổ vào lọ 2,5dl nước (trước đó trong lọ không có nước hoặc vật khác). Tính gần đúng khoảng cách k từ mặt nước trong lọ khi nước lặng yên đến mép trên của lọ (quy tròn số đến hàng phần trăm, nghĩa là làm tròn số đến hai chữ số sau dấu phảy).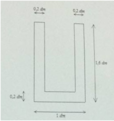
![]()
![]()
![]()
![]()