Ở 20°C phản ứng aA + bB → cC +dD kết thúc sau 40 phút. Nếu thực hiện phản ứng ở 50°C thì phản ứng sẽ kết thúc sau bao lâu? Biết rằng, cứ tăng thêm 10°C thì tốc độ phản ứng sẽ tăng lên 2 lần
A. 40 phút
B. 20 phút
C. 10 phút
D. 5 phút
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Theo định nghĩa, số lần tăng tốc độ phản ứng khi nhiệt độ thay đổi 100C chính là hệ số nhiệt độ γ.
Suy ra γ = 3.
Gọi nhiệt độ sau khi tăng là t2
Thay vào công thức ta có
81 = 3 ( 1 - 30 ) / 10 ⇔ ( t 2 - 30 ) 10 = 4 ⇔ t 2 = 70 0 C

Đáp án B
Theo định nghĩa, số lần tăng tốc độ phản ứng khi nhiệt độ thay đổi 100C chính là hệ số nhiệt độ γ.
Suy ra γ = 3.
Gọi nhiệt độ sau khi tăng là t2
Thay vào công thức ta có
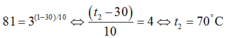

Đáp án D
Theo định nghĩa, số lần tăng tốc độ phản ứng khi nhiệt độ thay đổi 10°C chính là hệ số nhiệt độ g
Suy ra g = 3.
Thay vào công thức ta có tỉ số tốc độ phản ứng:
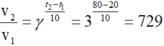
Vậy tốc độ phản ứng tăng 729 lần khi nhiệt độ tăng từ 20°C tới 80°C.

Đáp án D
Theo định nghĩa, số lần tăng tốc độ phản ứng khi nhiệt độ thay đổi 10°C chính là hệ số nhiệt độ g
Suy ra g = 3.
Thay vào công thức ta có tỉ số tốc độ phản ứng:

Vậy tốc độ phản ứng tăng 729 lần khi nhiệt độ tăng từ 20°C tới 80°C.

\(v_{thuận}=k_{thuận}\left[A\right]^a\left[B\right]^b\\ v_{nghịch}=k_{nghịch}\left[C\right]^c\left[D\right]^d\\\dfrac{k_{thuận}}{k_{nghịch}} =\dfrac{\left[C\right]^c\left[D\right]^dv_{thuận}}{\left[A\right]^a\left[B\right]^bv_{nghịch}}\)
aA+bB ⇌ cC + dD
- Tốc độ phản ứng thuận ở trạng thái cân bằng: \({{\rm{v}}_{\rm{t}}}{\rm{ = }}{{\rm{k}}_{\rm{t}}}{{\rm{(A)}}^{\rm{a}}}{{\rm{(B)}}^{\rm{b}}}\)
- Tốc độ phản ứng nghịch ở trạng thái cân bằng: \({{\rm{v}}_{\rm{n}}}{\rm{ = }}{{\rm{k}}_{\rm{n}}}{{\rm{(C)}}^{\rm{c}}}{{\rm{(D)}}^{\rm{d}}}\)
- Ở trạng thái cân bằng, tốc độ phản ứng thuận bằng tốc độ phản ứng nghịch:
\(\begin{array}{l}{\rm{ }}{{\rm{v}}_{\rm{t}}}{\rm{ = }}{{\rm{v}}_{\rm{n}}}\\ \Leftrightarrow {{\rm{k}}_{\rm{t}}}{{\rm{(A)}}^{\rm{a}}}{{\rm{(B)}}^{\rm{b}}}{\rm{ = }}{{\rm{k}}_{\rm{n}}}{{\rm{(C)}}^{\rm{c}}}{{\rm{(D)}}^{\rm{d}}}\end{array}\)
\( \Rightarrow \)\(\frac{{{{\rm{k}}_{\rm{t}}}}}{{{{\rm{k}}_{\rm{n}}}}} = \frac{{{{{\rm{(C)}}}^{\rm{c}}}{{{\rm{(D)}}}^{\rm{d}}}}}{{{{{\rm{(A)}}}^{\rm{a}}}{{{\rm{(B)}}}^{\rm{b}}}}}\)
Chọn B