Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.A'B'C'D' có A trùng với gốc tọa độ O, các đỉnh
B
m
;
0
;
0
,
D
0
;
m
;
0
,
A
'
0
;
0
;
n
với
m
,
n
>
0
và
m
+
n
=
4
. Gọi M là trung điểm của cạnh CC'. Khi đó thể tích tứ diện BDA'M đạt giá...
Đọc tiếp
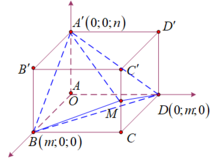
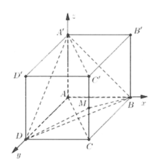
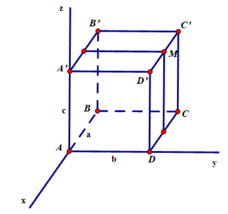
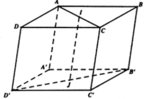
Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.A'B'C'D' có A trùng với gốc tọa độ O, các đỉnh B m ; 0 ; 0 , D 0 ; m ; 0 , A ' 0 ; 0 ; n với m , n > 0 và m + n = 4 . Gọi M là trung điểm của cạnh CC'. Khi đó thể tích tứ diện BDA'M đạt giá trị lớn nhất bằng:
A. 245 108
B. 9 4
C. 64 27
D. 75 32
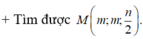
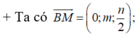
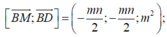
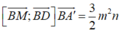
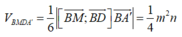
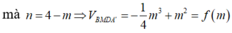
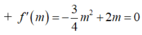
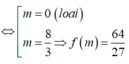
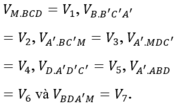
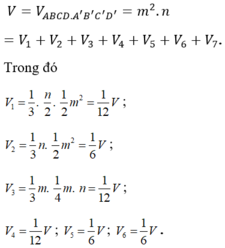
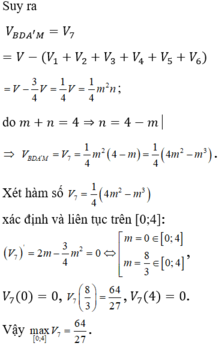
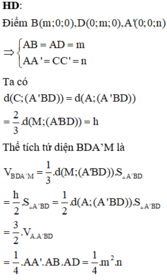
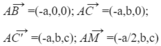
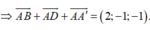
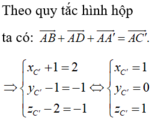
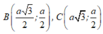
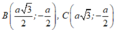
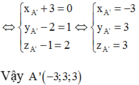
Đáp án là C.
+ Tìm được M m ; m ; n 2 .
+ Ta có:
B M → = 0 ; m ; n 2 ; B D → = − m ; m ; 0 ; B A ' → = − m ; 0 ; n
B M → ; B D → = − m n 2 ; − m n 2 ; m 2 ; B M → ; B D → B A ' → = 3 2 m 2 n
V B M D A ' = 1 6 B M → ; B D → B A ' → = 1 4 m 2 n
mà n = 4 − m ⇒ V B M D A ' = − 1 4 m 3 + m 2 = f m
+ f ' m = − 3 4 m 2 + 2 m = 0 ⇔ m = 0 l o a i m = 8 3 ⇒ f m = 64 27