Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi M, N lần lượt là trung điểm của AB, CD
Ta có: Δ B C D = Δ A C D ⇔ B N = A N ⇒ Δ A B N cân
⇒ M N ⊥ A B
Tương tự, ta chứng minh được M N ⊥ C D ⇒ M N là đoạn vuông chung của AB và
CD.
Xét tam giác ABN có: A N = B N = a 3 2 ; A B = a
M N = A N 2 − A M 2 = A N 2 − A B 2 4 = a 3 2 2 − a 2 4 = a 2 2
Vậy khoảng cách giữa hai đường thẳng AB, CD là: a 2 2

Chọn đáp án A
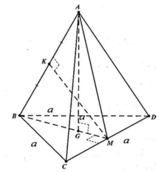
Gọi G là trọng tâm tam giác BCD => AG ⊥ (BCD)
Gọi M là trung điểm CD => BM ⊥ CD

Kẻ MK ⊥ AB (K ∈ AB)
Mặt khác MK ⊥ CD vì CD ⊥ (SBM)
=> MK là đường vuông góc chung.
=> d(AB;CD) = MK![]()
Khi đó M là trung điểm AB
![]()
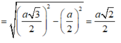
Vậy khoảng cách giữa AB và CD bằng
Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
Ta có: