Cho số thực a bất kì và giả sử f là môt hàm liên tục. Hỏi mệnh đề nào sau đây đúng?
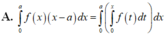
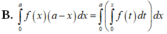
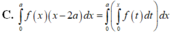
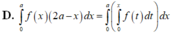
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt F x = ∫ 0 x f t d t . Ta cần chứng minh ∫ 0 a f x x - a d x = ∫ 0 a F x d x
Ta có F'(x) = f(x). Khi đó
∫ 0 a f x a - x d x = a ∫ 0 a f x d x - ∫ 0 a x f x d x = a F a - ∫ 0 a x F ' x d x
Sử dụng công thức tích phân từng phần, ta có ∫ 0 a x F ' x d x = a F a - ∫ 0 a F x d x
Thay vào ta thu được kết quả ở B
Đáp án B

Theo tính chất tích phân ta có:
+ ) ∫ a b f ( x ) d x + ∫ b c f ( x ) d x + ∫ c a f ( x ) d x
∫ c a f ( x ) d x + ∫ c a f ( x ) d x = ∫ a a f ( x ) d x = 0
Đáp án A đúng.
+ ) ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x
với
c
∈
ℝ
.Đáp án B đúng.
+ ) ∫ a b ( f ( x ) - g ( x ) ) d x + ∫ a b g ( x )
= ∫ b a f ( x ) d x - ∫ a b g ( x ) d x + ∫ a b g ( x ) d x = ∫ a b f ( x ) d x
Đáp án D đúng.
Đáp án C sai.
Chọn đáp án C.
Đáp án B