Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện 2 z 2 + 5 z + z ¯ = 0 là đường tròn nào dưới đây ?
A. x - 5 2 2 + y 2 = 25 4
B. x 2 + y 2 = 25 4
C. x + 5 2 2 + y 2 = 25 4
D. x - 2 5 2 + y 2 = 25 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Gọi z = x ; y khi đó điều kiện trở thành:
x 2 + y − 1 2 = x 2 + y + 1 2 ⇔ y = − 1
Như vậy quỹ tích là một đường thẳng.

Đáp án A.
Gọi
z
=
x
;
y
khi đó điều kiện trở thành ![]() .
.
Như vậy quỹ tích là một đường thẳng

Đáp án A
Giả sử z = x + y i
Ta có z - 1 + i = z + 2 i ⇔ x - 1 2 + y - 1 2 = x 2 + y + 2 2 ⇔ x + 3 y + 1 = 0
Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 1 + i = z + 2 i là đường thẳng

Đáp án A
Giả sử z = x + yi
Ta có ![]()
![]()
![]()
Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện |z-(1+i)| = |z+2i| là đường thẳng

Giả sử M, N là điểm biểu diễn số phức z 1 , z 2 theo giả thiết suy ra M, N nằm trên đường tròn tâm I(5;3) bán kính r = 5 và MN là dây cung có độ dài bằng 8. Do đó trung điểm A của MN nằm trên đường tròn tâm I bán kính r' = 3.

Chọn C.

Chọn C.
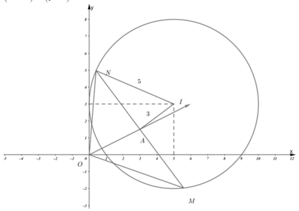
Phương pháp: Sử dụng phép biến hình.
Cách giải: Giả sử M, N là điểm biểu diễn số phức z 1 , z 2 theo giả thiết suy ra M, N nằm trên đường tròn tâm I(5;3) bán kính r = 5 và MN là dây cung có độ dài bằng 8. Do đó
trung điểm A của MN nằm trên đường tròn tâm I bán kính r' = 3.


Chọn C.