Trong không gian Oxyz, cho mặt cầu (S): x 2 + ( y - 3 ) 2 + ( y + 4 ) 2 = 4 . Xét hai điểm M,N di động trên (S) sao cho MN=1 Giá trị nhỏ nhất của O M 2 - O N 2 bằng
A. -10
B. - 4 - 3 5
C. -5
D. - 6 - 2 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

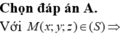
( x + 5 ) 2 + ( y + 5 ) 2 + ( z - 14 ) 2 = 324
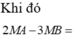
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dấu bằng đạt tại
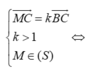
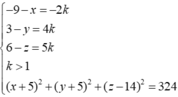
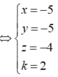

Xét điểm M(x;y;z), N(a;b;c) ta có
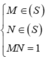
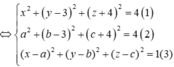
Lấy (1) – (2) theo vế có: ![]()
![]()
Kết hợp sử dụng bất đẳng thức Cauchy – Schwarz (Bunhiacopski) và (3) ta có
![]()
![]()
![]()
![]() =-10
=-10
Dấu bằng đạt tại 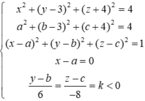
Chọn đáp án A.
*Một cách tương tự mở rộng cho min –max của α O M 2 + β O N 2 .

Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.

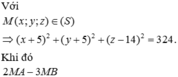
= 2 x + 14 2 + y - 13 2 + z + 4 2 - 3 x + 7 2 + y + 1 2 + z - 1 2 = 4 x + 14 2 + y - 13 2 + z + 4 2 + 5 x + 5 2 + y + 5 2 + z - 14 2 - 324 - 3 x + 7 2 + y + 1 2 + z - 1 2 = 3 x + 9 2 + y - 3 2 + z - 6 2 - x + 7 2 + y + 1 2 + z - 1 2


Đáp án A.