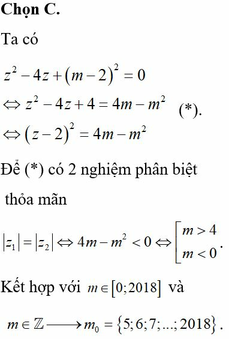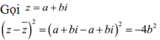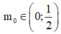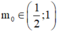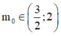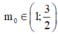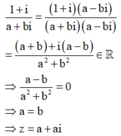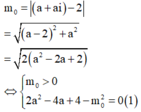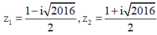Trong tập các số phức, cho phương trình z 2 - 4 z + m - 2 2 = 0 , m ∈ ℝ 1 Gọi m 0 là một giá trị của m để phương trình (1) có hai nghiệm phân biệt z 1 , z 2 thỏa mãn . Hỏi trong đoạn z 1 = z 2 có bao nhiêu giá trị nguyên của ?
A. 2019
B. 2015
C. 2014
D. 2018