Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y=f(2-x) đồng biến trên khoảng
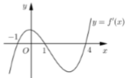
A. (1;3)
B. (2; + ∞ )
C. (-2;1)
D. - ∞ ; - 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.
.
.
.
CM
28 tháng 9 2018
Dùng đặc biệt hóa. Ta thử các giá trị cụ thể của x để xét sự đồng biến với lưu ý hàm số đồng biến thì x 1 > x 2 ⇒ f x 1 > f x 2 trên mỗi khoảng đang xét.
Đáp án cần chọn là C
CM
21 tháng 7 2017
Ta có:( f( 2-x) )’= ( 2-x)’.f’(2-x) = -f’(2-x)
Hàm số đồng biến khi
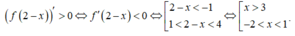
Chọn D.
CM
27 tháng 2 2017
Chọn C
+ Áp dụng công thức đạo hàm của hàm hợp ta có:
g’( x) = ( 2-x)’. f’( 2-x) = -f’( 2-x)
+ Nhận xét: Hàm số y= f( x) đã cho nghịch biến trên các khoảng (- ∞; -1) và ( 1;4) ( trên 2 khoảng đó f’(x) < 0) .
+ Hàm số đồng biến khi và chỉ khi
CM
6 tháng 1 2019
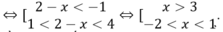
Đáp án A
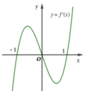
Phương pháp:
Tính y’, giải bất phương trình y’>0
Cách giải:
Với
Đáp án C.
Dựa vào đồ thị của hàm số
Ta có (f(2-x))'=-f '(2-x)
Để hàm số y=f(2-x) đồng biến thì: