Tính diện tích hình thang vuông có \(\widehat{A}=\widehat{D}=90^{0^{ }}\) ,AB = 2cm, CD = BC = 5cm ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 6 2017
Kẻ đường cao BH (H thuộc CD).
Khi đó Tứ giác ABHD là hình vuông (Tứ giác có 3 góc vuông và hai cạnh kề bằng nhau).
Suy ra BH = AB = 2
Trong tam giác vuông BHC có BH =1/2 BC nên tam giác BHC là nửa tam giác đều.
Suy ra \(\widehat{HBC}=60^0va\widehat{C}=30^o\)
Vậy các góc của hình thang là: \(\widehat{A}=\widehat{D}=90^o;\widehat{B}=150^o;\widehat{C}=30^o\)
4 tháng 9 2018
Kẻ \(BH\perp CD\)
Mà \(CD\perp AD\left(gt\right)\Rightarrow BH//AD\)
Hình thang ABHD (AB//HD) có BH//AD nên \(\hept{\begin{cases}HD=AB=5\left(cm\right)\\BH=AD\end{cases}}\) (t/c hình thang)
\(HD+HC=DC\Rightarrow5+HC=9\Rightarrow HC=4\left(cm\right)\)
\(\Delta HBC\)vuông cân tại H nên \(HB=HC=4cm\Rightarrow AD=4cm\left(AD=BH\right)\)
Áp dụng định lí Pitago tính được \(BC=\sqrt{32}\left(cm\right)\)
Chu vi hình thang vuông ABCD là:
\(AB+BC+CD+AD=5+\sqrt{32}+9+4=18+\sqrt{32}\left(cm\right)\)
Chúc bạn học tốt.
A
21 tháng 1 2021
Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2
21 tháng 1 2021
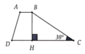
Kẻ BH \(\perp\) CD tại H
Xét tam giác BHC vuông tại H (BH \(\perp\) CD): \(\widehat{C}\) = 30o
\(\Rightarrow\) BH = \(\dfrac{1}{2}\)BC (Tính chất cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
hay BH = \(\dfrac{1}{2}\).8 = 4(cm)
Vì ABCD là hình thang (AB // CD)
\(\Rightarrow\) SABCD = \(\dfrac{1}{2}\)(AB + CD).BH = \(\dfrac{1}{2}\).(2 + 9).4 = 22 (cm2)
Chúc bn học tốt!
Kẻ BH⊥CD thì BH//AD, BH⊥AB
BH//AD và AB//HD nên ABHD là hbh
\(\Rightarrow AB=DH=2\left(cm\right);AD=BH\\ \Rightarrow CH=CD-DH=3\left(cm\right)\)
Pytago: \(AD^2=BH^2=BC^2-DH^2=16\left(cm\right)\)
\(\Rightarrow AD=4\left(cm\right)\\ \Rightarrow S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=\dfrac{1}{2}\cdot4\cdot7=14\left(cm^2\right)\)
ủa DH hay CH vậy a ?