- Cho 3 điểm A B C cùng nằm trên một đoạn thẳng . Biết độ dài AB là 8cm BC là 4cm.tính chu vi hình tròn có đường kính AB BC AC. Tính S phần thuộc hình tròn đường kính AC nhưng ko thuộc các hình tròn còn lại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2017
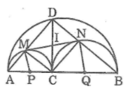
Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: CD ≤ OD nên MN ≤ OD
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.
5 tháng 1 2021
a) Gọi O là trung điểm của AD
mà AD là đường kính
nên O là tâm của đường tròn đường kính AD
hay OA=OD=R
Ta có: ΔACD vuông tại C(AC⊥CD)
mà CO là đường trung tuyến ứng với cạnh huyền AD(O là trung điểm của AD)
nên \(CO=\dfrac{AD}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(OA=OD=\dfrac{AD}{2}\)(O là trung điểm của AD)
nên OC=OA=OD(1)
Ta có: ΔABC cân tại A(gt)
mà AH là đường cao ứng với cạnh đáy BC(gt)
nên AH là đường phân giác ứng với cạnh BC(Định lí tam giác cân)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)
hay \(\widehat{BAD}=\widehat{CAD}\)
Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(cmt)
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
⇒\(\widehat{ABD}=\widehat{ACD}\)(hai góc tương ứng)
mà \(\widehat{ACD}=90^0\)(AC⊥CD)
nên \(\widehat{ABD}=90^0\)
hay AB⊥BD
Ta có: ΔABD vuông tại B(AB⊥BD)
mà BO là đường trung tuyến ứng với cạnh huyền AD(O là trung điểm của AD)
nên \(BO=\dfrac{AD}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AO=OD=\dfrac{AD}{2}\)(O là trung điểm của AD)
nên OB=OD=OA(2)
Từ (1) và (2) suy ra OB=OC=R
⇒B,C cùng thuộc đường tròn(O)
hay B,C cùng thuộc đường tròn đường kính AD(đpcm)
CM
13 tháng 11 2019
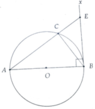
a, Tính được BC=5cm
AC = 5 3 cm; CE = 5 3 3 cm
b, Tính được BE = 10 3 3 cm