Cho lăng trụ đứng có chiều cao bằng h không đổi, một đáy là tứ giác ABCD với A ,B ,C ,D di động. Gọi I là giao của hai đường chéo AC và BD của tứ giác đó. Cho biết IA.IC = IB.ID = h 2 . Tính giá trị nhỏ nhất bán kính mặt cầu ngoại tiếp hình lăng trụ đã cho.
![]()
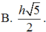
![]()
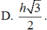

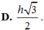
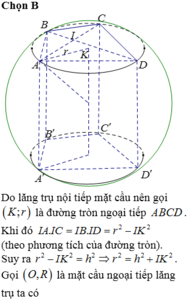
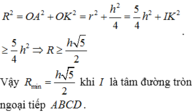
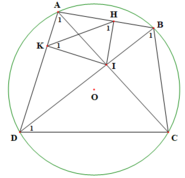
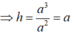
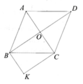
Đáp án đúng : B