Cho hình chóp S.ABC có đáy là tam giác vuông tại A, mặt bên (SBC) là tam giác đều và nằm trong mặt phẳng vuông góc đáy (tham khảo hình vẽ bên). Tang góc giữa đường thẳng SA và mặt phẳng (ABC) bằng
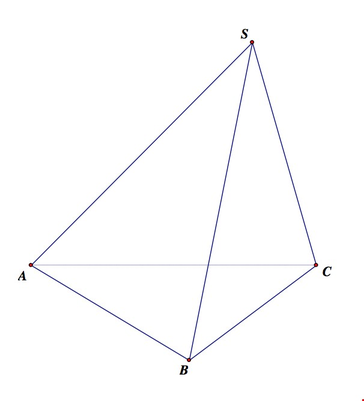
A. 3
B. 6 3
C. 6 2
D. 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
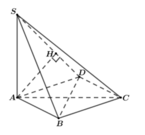
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
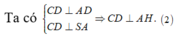
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
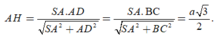
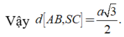

Đáp án C
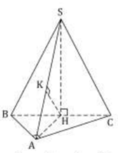

Từ (1), (2) => HK là đoạn vuông góc chung của SA và BC

Tam giác SHA vuông tại A có đường cao HK nên 1 HK 2 = 1 SH 2 + 1 AH 2 = 4 3 a 2 + 4 a 2 = 16 3 a 2 .
⇒ HK = 3 a 4 .

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.