Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C và SA ⊥ (ABC). Biết SA = BC = a, AB = a 3 , tính khoảng cách h từ A tới mặt phẳng (SBC).
A. h = a 3 2
B. h = a 3 2
C. h = a 2 3
D. h = a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
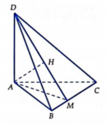
Trong mặt phẳng (ABC) Kẻ A M ⊥ B C
Trong mặt phẳng (SAM) kẻ A H ⊥ S M
⇒ d A ; S B C = A H
Ta có A M = A B . cos B A M ^ = A B . cos 60 0 = a 2
Diện tích tam giác ABC là S A B C = 1 2 A B . A C . sin 120 0 = 1 2 a 2 3 2 = a 2 3 4 Ta có
V S . A B C = 1 3 . S A . S A B C = 1 3 . S A . a 3 3 24 = a 3 3 24 ⇒ S A = a 2
Tam giác SAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 S A 2 + 1 A M 2 ⇒ A H = a 2 4

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.

Đáp án A
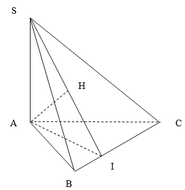
Gọi I, H lần lượt là hình chiếu của A lên BC và SI
Ta có: 1 A I 2 = 1 A B 2 + 1 A C 2 = 1 2 a 2 + 1 3 a 2 = 13 36 a 2
1 A H 2 = 1 S A 2 + 1 A I 2 = 1 4 a 2 + 1 36 a 2 = 61 144 a 2
⇒ A I = 12 a 61 ⇒ d = A I = 12 a 61

Đáp án B
HDG:
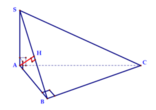
![]()
Dễ dàng chứng minh ∆ S B C vuông tại B
![]()
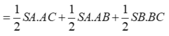
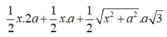
![]()
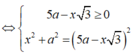
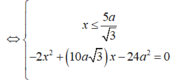
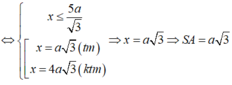
Ta có (SAB) ⊥ (SBC) theo giao tuyến SB. Kẻ
![]()
![]()
Đáp án B