Cho hình chop S.ABC đáy ABC là tam giác đều, cạnh bên SA vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AB và SB. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. C M ⊥ S B
B. CM ⊥ AN
C. MN ⊥ MC
D. AN ⊥ BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Sử dụng quan hệ vuông góc để chứng minh các đáp án và chọn đáp án đúng.
Cách giải:
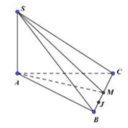
ABC là tam giác cân tại A, M là trung điểm của BC
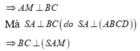
Chọn: C

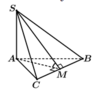
Gọi M là trung điểm BC, suy ra A M ⊥ B C
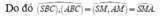
Tam giác ABC đều cạnh a suy ra trung tuyến ![]()
Tam giác vuông SAM có ![]()
Chọn D.

Chọn D.
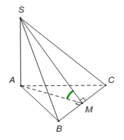
Gọi M là trung điểm của BC, suy ra AM ⊥ BC.
Ta có
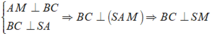
Do đó
![]()
Tam giác ABC đều cạnh a, suy ra trung tuyến AM = a 3 2
Tam giác vuông SAM, có
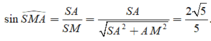

Đáp án D
Kẻ Ax//BC, H I ⊥ A x , H K ⊥ S I . Gọi M là trung điểm của AB
⇒ d ( B C , S A ) = d ( B C , ( S A x ) ) = 4 3 d ( H , S A x )
Ta có A I ⊥ ( S H I ) ⇒ A I ⊥ H K ⇒ H K ⊥ ( S A I ) ⇒ d ( H , ( S A x ) ) = H K
Góc giữa SC và (ABC) là góc S C H ^ = 60 °
Ta có H C = C M 2 + M H 2 = a 3 2 2 + a 4 2 = a 13 4
⇒ S H = H C . tan 60 ° = a 39 4
H I = A H . sin 60 ° = 3 4 . a . 3 2 = a . 3 3 8
Ta có H K 2 = H I 2 . S H 2 H I 2 + S H 2 = 351 . a 2 61 ⇒ H K = a 351 61
⇒ d ( B C , S A ) = 4 3 . d H , ( S A x ) = 4 a 351 3 61

Đáp án A
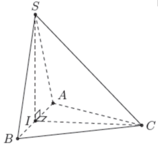
Ta có S A = S B và C A = C B nên Δ S A C = Δ S B C
Ta có I C ⊥ A B A B C ⊥ S A B suy ra I C ⊥ S A B
Chứng minh tương tự ta có S I ⊥ A B C