Cho phương trình
8 z 2 - 4 a + 1 z + 4 a + 1 = 0
với a là tham số. Tìm a ∈ ℝ để phương trình có hai nghiệm z 1 ; z 2 thỏa mãn z 1 z 2 là số ảo, trong đó z 2 là số phức có phần ảo dương.
A. a = 0
B. a = 2
C. a ∈ 0 ; 2
D. a ∈ 0 ; 1 ; 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4

a) \(x^2-mx+2m-4=0\) nhận \(x=3\) là nghiệm nên:
\(3^2-m.3+2m-4=0\)
\(\Leftrightarrow9-3m+2m-4=0\)
\(\Leftrightarrow m-5=0\)
\(\Leftrightarrow m=5\)
Vậy phương trình trở thành: \(x^2-5x+6=0\) nhận x=3 là nghiệm vậy nghiệm còn lại là:
\(\Delta=\left(-5\right)^2-4.1.6=1\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)+\sqrt{1}}{2.1}=3\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)-\sqrt{1}}{2.1}=2\end{matrix}\right.\)
Vậy nghiệm còn lại là \(x=2\)

a, x 2 − 2 ( m + 1 ) x + m 2 + m − 1 = 0 (1)
Với m = 0, phương trình (1) trở thành:
x 2 − 2 x − 1 = 0 Δ ' = 2 ; x 1 , 2 = 1 ± 2
Vậy với m = 2 thì nghiệm của phương trình (1) là x 1 , 2 = 1 ± 2
b) Δ ' = m + 2
Phương trình (1) có hai nghiệm phân biệt ⇔ m > − 2
Áp dụng hệ thức Vi-ét, ta có: x 1 + x 2 = 2 ( m + 1 ) x 1 x 2 = m 2 + m − 1
Do đó:
1 x 1 + 1 x 2 = 4 ⇔ x 1 + x 2 x 1 x 2 = 4 ⇔ 2 ( m + 1 ) m 2 + m − 1 = 4 ⇔ m 2 + m − 1 ≠ 0 m + 1 = 2 ( m 2 + m − 1 ) ⇔ m 2 + m − 1 ≠ 0 2 m 2 + m − 3 = 0 ⇔ m = 1 m = − 3 2
Kết hợp với điều kiện ⇒ m ∈ 1 ; − 3 2 là các giá trị cần tìm.

Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1

Chọn B.
Từ giả thiết suy ra z1; z2 không phải là số thực.
Do đó Δ’ < 0, hay 4( a + 1)2 - 8(4a + 1) < 0
Hay a2 - 6a -1 < 0 (*)
Suy ra 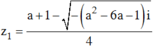 ,
,
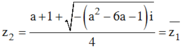
Ta có z1/ z2 là số ảo khi và chỉ khi ![]() là số ảo
là số ảo
Tương đương: (a + 1)2 - (-(a2 - 6a - 1)) = 0 hay a2 - 2a = 0
Vậy a = 0 hoặc a = 2.
Đối chiếu với điều kiện (*) ta có giá trị của a là a = 0 hoặc a = 2.

a: Thay m=3 vào pt, ta được:
\(x^2-2\cdot\left(3-1\right)x+3^2-2\cdot3=0\)
\(\Leftrightarrow x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>x=1 hoặc x=3
b: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-2m\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-2m\right)\)
\(=4m^2-8m+4-4m^2+8m=4>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Thay x=-2 vào pt, ta được:
\(\left(-2\right)^2-2\cdot\left(-2\right)\cdot\left(m-1\right)+m^2-2m=0\)
\(\Leftrightarrow m^2-2m+4+4\left(m-1\right)=0\)
\(\Leftrightarrow m^2-2m+4+4m-4=0\)
=>m(m+2)=0
=>m=0 hoặc m=-2
Theo hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2-2=2\cdot\left(-1\right)=-2\\x_2-2=2\cdot\left(-3\right)=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=0\\x_2=-4\end{matrix}\right.\)
c: \(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-2m\right)=4\)
\(\Leftrightarrow4m^2-8m+4-2m^2+4m-4=0\)
\(\Leftrightarrow2m^2-4m=0\)
=>2m(m-2)=0
=>m=0 hoặc m=2

a, \(\Delta=m^2-4\left(-4\right)=m^2+16\)> 0
Vậy pt luôn có 2 nghiệm pb
b, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-4\end{matrix}\right.\)
Ta có \(\left(x_1+x_2\right)^2-2x_1x_2=5\)
Thay vào ta được \(m^2-2\left(-4\right)=5\Leftrightarrow m^2+3=0\left(voli\right)\)
Bạn ơi, mình có thể hỏi câu c được không ạ? Nếu không được thì không sao, mình cảm ơn câu trả lời của bạn ạ ^-^ chúc bạn một ngày tốt lành nhé.
Từ giả thiết suy ra z 1 ; z 2 không phải là số thực. Khi đó
∆ ' < 0 ⇔ a + 1 2 - 8 4 a + 1 ⇔ 4 a 2 - 6 a - 1 < 0
Suy ra
z 1 = a + 1 - - a 2 - 6 a + 1 t 2 4 z 2 = a + 1 - a 2 - 6 a + 1 t 2 4
z 1 z 2 là số ảo z 1 2 là số ảo
⇔ a + 1 2 - - a 2 - 6 a - 1 ⇔ a 2 - 2 a = 0 ⇔ a = 0 a = 2
Thay vào điều kiện (*) thấy thỏa mãn.
Đáp án C