Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x − 2 y − 2 z = 0 và điểm A 2 ; 2 ; 0 . Viết phương trình mặt phẳng O A B , biết rằng điểm B thuộc mặt cầu (S), có hoành độ dương và tam giác OAB đều.
A. x − y − 2 z = 0
B. x − y + z = 0
C. x − y − z = 0
D. x − y + 2 z = 0



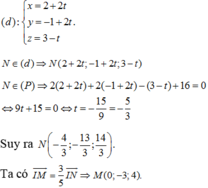

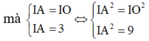
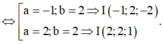
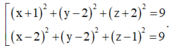



Đáp án C.
Đặt B x ; y ; z . Ta có O A 2 = 8, Δ O A B đều ⇒ O A 2 = O B 2 = A B 2 = 8 .
Mà B ∈ S ⇒ Ta có hệ x 2 + y 2 + z 2 − 2 x − 2 y − 2 z = 0 1 x 2 + y 2 + z 2 = 8 (2) x − 2 2 + y − 2 2 + z 2 = 8 (3)
Thế (2) vào (1) và (3) ta được: x + y + z = 4 x + y = 2 ⇔ z = 2 y = 2 − x .
Thế vào (2):
x 2 + 2 − x 2 = 8 ⇔ 2 x 2 − 4 x = 0 ⇔ x = 0 l x = 2
Với x = 2 ⇒ y = 0 ⇒ B 2 ; 0 ; 2
⇒ n → = O A → , O B → = 4 ; − 4 ; − 4 ⇒ Phương trình O A B : x − y − z = 0 .