Hình chóp S.ABC có SA, SB, SC đôi một vuông góc. Biết SA = SB = 2a, SC = a. Gọi G là trọng tâm ∆ ABC. Tính SG
A. SG = 1 3 a 2 3
B. SG = a 2
C. SG = 2 a 3
D. SG = a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này ứng dụng bài toán đồng phẳng đã chứng minh cho em hồi sáng:
4 điểm M, A', B', C', D' đồng phẳng nên với điểm S bất kì ta có:
\(\overrightarrow{SM}=m.\overrightarrow{SA'}+n.\overrightarrow{SB'}+p.\overrightarrow{SC'}\)
Khi đó \(m+n+p=1\)
Giải như sau:
Đặt \(\dfrac{SA}{SA'}=x;\dfrac{SB}{SB'}=y;\dfrac{SC}{SC'}=z\)
\(\Rightarrow\overrightarrow{SA}=x.\overrightarrow{SA'};\overrightarrow{SB}=y.\overrightarrow{SB'};\overrightarrow{SC}=z.\overrightarrow{SC'}\)
Do G là trọng tâm ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{GS}+\overrightarrow{SA}+\overrightarrow{GS}+\overrightarrow{SB}+\overrightarrow{GS}+\overrightarrow{SC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SG}\)
\(\Rightarrow x.\overrightarrow{SA'}+y.\overrightarrow{SB'}+z.\overrightarrow{SC'}=3\overrightarrow{SG}=6\overrightarrow{SM}\) (do M là trung điểm SG)
\(\Rightarrow\dfrac{x}{6}.\overrightarrow{SA'}+\dfrac{y}{6}.\overrightarrow{SB'}+\dfrac{z}{6}.\overrightarrow{SC'}=\overrightarrow{SM}\)
Do M;A';B';C' đồng phẳng
\(\Rightarrow\dfrac{x}{6}+\dfrac{y}{6}+\dfrac{z}{6}=1\) \(\Rightarrow x+y+z=6\)
\(\Rightarrow\dfrac{SA}{SA'}+\dfrac{SB}{SB'}+\dfrac{SC}{SC'}=6\)
Với bài toán trắc nghiệm (hoặc cần kiểm chứng kết quả) chỉ cần chọn trường hợp đặc biệt là (P) song song đáy, khi đó theo Talet thì A', B', C' lần lượt là trung điểm các cạnh nên ta dễ dàng tính ra tổng cần tính là 2+2+2=6

Phương pháp:
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
S.ABC là tứ diện vuông tại đỉnh S
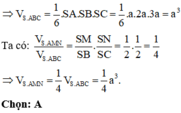
Đáp án D