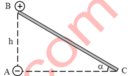
Quả cầu nhỏ khối lượng m mang điện tích +q trượt không ma sát với vận tốc v 0 = 0 tại đỉnh B có độ cao h của mặt phẳng nghiêng BC. Tại đỉnh góc vuông A của tam giác ABC có một điện tích –q . Giá trị nhỏ nhất của α để quả cầu có thể tới được C là:
A. tan α min = m g h 2 k q 2
B. tan α min = 1 − m g h 2 k q 2
C. tan α min = m g h k q
D. tan α min = 1 − m g h k q

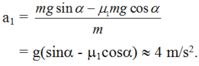
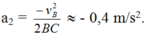
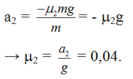
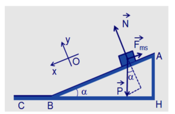
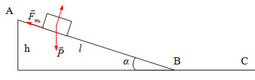
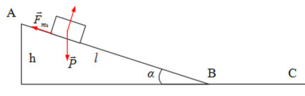

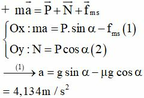
Chọn gốc thế năng ở chân mặt phẳng nghiêng; mốc thế năng điện ở vô cùng. Khi đó năng lượng của điện tích +q:
Tại B: E B = 0 ⏟ E d = 0 + m g h + − k q 2 h .
Tại C: E C = 1 2 m v 2 + 0 ⏟ E t = 0 + − k q 2 A C = 1 2 m v 2 + − k q 2 tan α h .
Áp dụng bảo toàn cơ năng E B = E C ⇒ v = 2 g h − 1 − tan α k q 2 m h .
Để quả cầu có thể C thì v ≥ 0 ⇒ tan α ≥ 1 − m g h 2 k q 2 .
Đáp án B