Đạo hàm của hàm số y= (x3-2x2)2 bằng
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

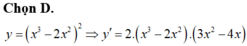
![]()
![]()
![]()

Đáp án C
Phương pháp: Sử dụng công thức tính đạo hàm của hàm hợp: ![]()
Cách giải:
![]()
![]()
![]()

Chọn B.
Đặt u = x 3 − 2 x 2 thì y = u 2016 , y ' u = 2016. u 2015 , u ' x = 3 x 2 − 4 x .
Theo công thức tính đạo hàm của hàm số hợp, ta có: y ' x = y ' u . u ' x .
Vậy: y'= 2016. ( x 3 − 2 x 2 ) 2 015 . ( 3 x 2 − 4 x ) .

Đáp án A
Đặt f 1 = a f ' 1 = b , thay x = 0 vào giả thiết, ta được f 2 1 = - f 3 0 ⇔ a 3 + a 2 = 0 ⇔ [ a = 0 a = - 1
Đạo hàm cả 2 vế biểu thức f 2 1 + 2 x = x - f 3 1 - x , ta đưuọc
4 f ' 1 + 2 x . f 1 + 2 x = 1 + 3 f ' 1 - x . f 2 1 - x 1
Thay x = 0 vào (1), ta có 4 f ' 1 . f 1 = 1 + 3 f ' 1 . f 2 1 ⇔ 4 a b = 1 + 3 a 2 b 2
TH1. Với a = 0 thay vào (2), ta được 0 = 1 (vô lí)
TH2. Với a = -1 thay vào (2), ta được - 4 b = 1 + 3 b ⇔ b = - 1 7 ⇒ f ' 1 = - 1 7
Vậy phương trình tiếp tuyến cần tìm là y - f 1 = f ' 1 x - 1 ⇒ y = - 1 7 x - 6 7 .

Áp dụng công thức u n ' = n u n − 1 . u ' .
Ta có
y ' = 2 x 5 − 2 x 2 x 5 − 2 x 2 ' = 2 x 5 − 2 x 2 5 x 4 − 4 x
= 2 ( 5 x 9 − 4 x 6 − 10 x 6 + 8 x 3 ) = 2 ( 5 x 9 − 14 x 6 + 8 x 3 ) = 10 x 9 − 28 x 6 + 16 x 3
Chọn đáp án C

\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị

Đáp án A
Ta có: f ( x ) = x 3 + 2 x 2 + 4 x + 5 ⇒ f ' x = 3 x 2 + 4 x + 4