Cho sin α = 1 3 và π 2 < α < π . Khi đó cos α có giá trị là:
A. - 2 3
B. 2 2 3
C. 8 9
D. - 2 2 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
3 tháng 4 2018
Đúng(0)
Những câu hỏi liên quan
26 tháng 7 2023
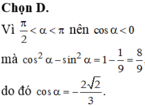
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
DN
1
18 tháng 1 2022
Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!
NN
1
11 tháng 5 2021
Bài 1 :
Ta có : a thuộc góc phần tư thứ II .
=> Cos a < 0
- Ta lại có : \(\left\{{}\begin{matrix}sina=\dfrac{1}{3}\\sin^2a+cos^2a=1\end{matrix}\right.\)
\(\Rightarrow cosa=\sqrt{1-\left(\dfrac{1}{3}\right)^2}=-\dfrac{2\sqrt{2}}{3}\)
Bài 2 :
Ta có : \(F=\dfrac{\cos x.\tan x}{\sin^2x-\cot x.\cos x}=\dfrac{\cos x.\dfrac{\sin x}{\cos x}}{\sin^2x-\dfrac{\cos x}{\sin x}.\cos x}\)
\(=\dfrac{\sin x}{\sin^2x-\dfrac{\cos^2x}{\sin x}}=\dfrac{1}{\sin x-\cot^2x}\)
N
1
12 tháng 8 2021
do a ∈ \(\left(0;\dfrac{\pi}{2}\right)\)⇒ \(\left\{{}\begin{matrix}sinx>0\\cosx>0\end{matrix}\right.\)
Mà tanx = 3 ⇒ \(\dfrac{sinx}{cosx}=3\Leftrightarrow\dfrac{sin^2x}{cos^2x}=9\Rightarrow10sin^2x=9\)
⇒ sinx = \(\dfrac{3}{\sqrt{10}}\)
⇒ sin (x + π) = -sinx = -\(\dfrac{3}{\sqrt{10}}\)
PT
1
PT
1
