Tìm số phức liên hợp của số phức z thỏa mãn (1+i)z = 1 + 3i
A. z ¯ = -1 + 2i
B. z ¯ = 1 - 2i
C. z ¯ = -1 - 2i
D. z ¯ = 1 + 2i
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2019
Chọn B.
Ta có: (2 - 3i).(1 + 2i) = 2 + 4i - 3i - 6i2 = 8 + i
Từ giả thiết : (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i nên
(1 + i)z + (8 + i) = 7 + 3i hay (1 + i)z = -1 + 2i
CM
28 tháng 11 2017
Đáp án D
Phương pháp:
Đặt z=a+bi, giải phương trình để tìm a, b
Cách giải: 
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 5 2021
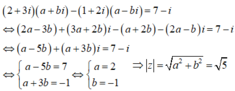
\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?
Đáp án C.